Рассмотрим тело, образованное вращением вокруг оси 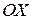 фигуры, ограниченной непрерывной кривой
фигуры, ограниченной непрерывной кривой 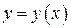 , осью
, осью 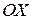 и прямыми
и прямыми 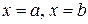 (рис. 7). Разобьем отрезок
(рис. 7). Разобьем отрезок 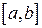 на
на 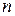 частей точками
частей точками 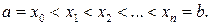 Проведем через точки деления плоскости, перпендикулярные оси
Проведем через точки деления плоскости, перпендикулярные оси 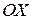 . Сечение тела вращения плоскостью
. Сечение тела вращения плоскостью 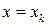 есть круг радиусом
есть круг радиусом 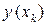 с площадью
с площадью 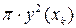
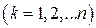 . Проведенные плоскости разобьют тело на слои. Каждый
. Проведенные плоскости разобьют тело на слои. Каждый 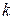 -й слой
-й слой
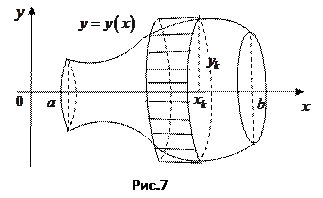
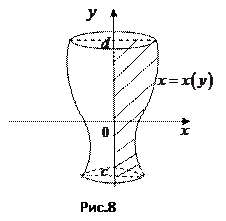
приближенно заменим прямым цилиндром (рис. 7) с радиусом 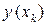 , высотой
, высотой 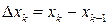 и объемом
и объемом 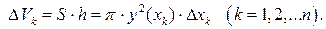
Сумма объемов всех цилиндров равна 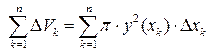 .
.
Объем тела вращения 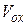 определяется как предел этой суммы
определяется как предел этой суммы
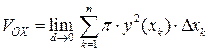
при стремлении к нулю величины 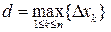 . Мы получили предел интегральной суммы непрерывной функции
. Мы получили предел интегральной суммы непрерывной функции 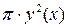 по отрезку
по отрезку 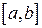 , который существует и равен интегралу
, который существует и равен интегралу 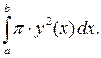
Итак, объем 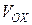 тела, полученного при вращении вокруг оси
тела, полученного при вращении вокруг оси 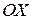 фигуры, ограниченной кривой
фигуры, ограниченной кривой 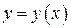 , осью
, осью 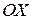 и прямыми
и прямыми 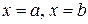 , вычисляется по формуле
, вычисляется по формуле
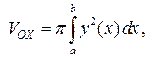 или
или 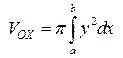 .
.
Аналогично вычисляется объем 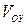 тела, полученного при вращении вокруг оси
тела, полученного при вращении вокруг оси  фигуры, ограниченной линией
фигуры, ограниченной линией 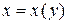 , осью
, осью  , прямыми
, прямыми 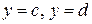 (рис. 8):
(рис. 8):
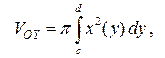 или
или 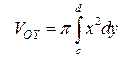 .
.
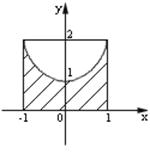
Пример 1. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями 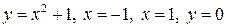 ,
,
а) вокруг оси 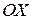 , б) вокруг оси
, б) вокруг оси  .
.
Решение. Построим параболу 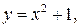 прямые
прямые 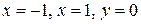 и заштрихуем фигуру, ограниченную этими линями (рис. 31).
и заштрихуем фигуру, ограниченную этими линями (рис. 31).
 а). Объем тела, полученного при вращении этой фигуры вокруг оси
а). Объем тела, полученного при вращении этой фигуры вокруг оси 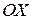 , вычислим по формуле:
, вычислим по формуле:
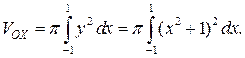
Подынтегральная функция − четная, поэтому используем следствие 2 к теореме.
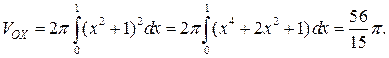
б). Для вычисления объема тела вращения фигуры вокруг оси  нельзя непосредственно воспользоваться формулой, так как фигура сверху ограничена не прямой, а параболой. Поэтому сначала рассмотрим фигуру, ограниченную прямой
нельзя непосредственно воспользоваться формулой, так как фигура сверху ограничена не прямой, а параболой. Поэтому сначала рассмотрим фигуру, ограниченную прямой 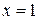 , осью
, осью  , прямыми
, прямыми 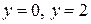 . При ее вращении вокруг оси
. При ее вращении вокруг оси  получим цилиндр, объем которого
получим цилиндр, объем которого 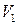 можно вычислить по формуле
можно вычислить по формуле 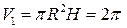 или по формуле
или по формуле 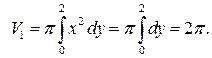
Теперь рассмотрим фигуру, ограниченную линиями 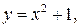 осью
осью  и прямой
и прямой 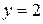 . При ее вращении вокруг оси
. При ее вращении вокруг оси  получим тело, объем которого
получим тело, объем которого 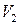 вычислим по формуле:
вычислим по формуле: 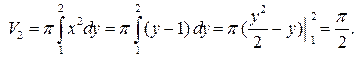
Тогда искомый объем 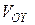 будет равен
будет равен 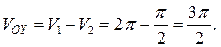
7. Лекционное занятие. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА
Случай 1. Пусть на плоскости дуга 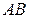 задана уравнением
задана уравнением 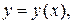
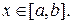 Будем предполагать, что функция
Будем предполагать, что функция 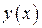 непрерывна вместе со своей производной на
непрерывна вместе со своей производной на 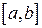 .
.
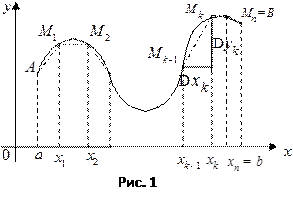
Рассмотрим на кривой точки 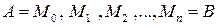 с абсциссами
с абсциссами 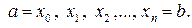 Проведем хорды
Проведем хорды 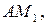
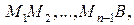 длины которых обозначим
длины которых обозначим 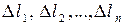 (рис. 1).
(рис. 1).
Вычислим длину 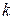 -й хорды
-й хорды
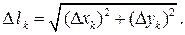
Для вычисления приращения 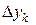 воспользуемся формулой конечных приращений Лагранжа
воспользуемся формулой конечных приращений Лагранжа
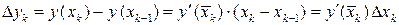 ,
,
где 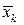 − некоторая точка из промежутка
− некоторая точка из промежутка 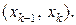 Тогда длина
Тогда длина 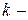 й хорды
й хорды
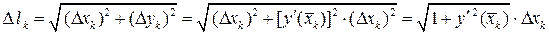 .
.
Учтем это и возьмем в определении криволинейного интеграла в качестве промежуточных точек на дугах 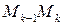 точки
точки 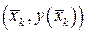 :
:
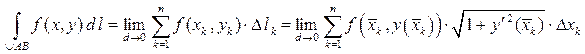 .
.
Мы получили предел интегральной суммы функции 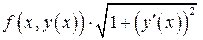 по отрезку
по отрезку 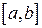 , который равен интегралу
, который равен интегралу 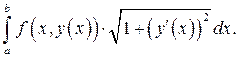 Следовательно,
Следовательно,
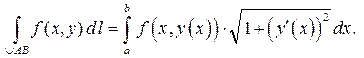
Итак, для вычисления криволинейного интеграла 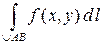 по дуге АВ с уравнением
по дуге АВ с уравнением 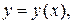
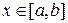 нужно:
нужно:
1) заменить 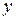 в подынтегральной функции на его значение
в подынтегральной функции на его значение 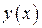 на дуге;
на дуге;
2) заменить 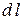 на
на 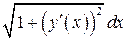 ;
;
3) вычислить получившийся определенный интеграл по отрезку 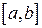 .
.
Иногда удобнее использовать уравнение кривой в виде 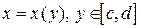 . Тогда
. Тогда
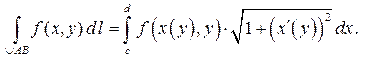
Пример 1. Вычислить длину дуги кривой
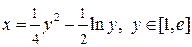 .
.
Решение. Уравнение кривой разрешено относительно  , поэтому воспользуемся формулой (7.16), учитывая, что
, поэтому воспользуемся формулой (7.16), учитывая, что 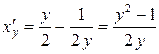 ,
,
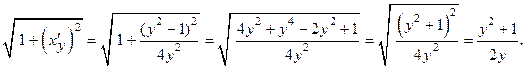
Тогда 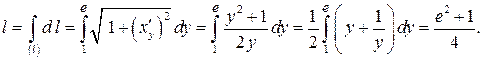
Случай 2. Пусть на плоскости дуга 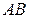 задана параметрическими уравнениями
задана параметрическими уравнениями
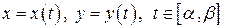 ,
,
причем функции 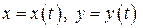 непрерывны на
непрерывны на 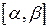 вместе со своими производными и
вместе со своими производными и 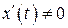 .
.
Для определенности, пусть 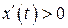 . Уравнения
. Уравнения 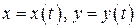 определяют функцию
определяют функцию 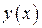 , которая имеет непрерывную производную
, которая имеет непрерывную производную 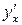 . Учитывая, что
. Учитывая, что 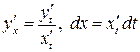 , получим
, получим 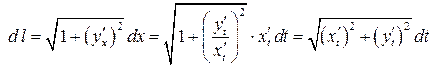 .
.
Итак, справедливы следующие формулы 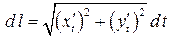 и
и
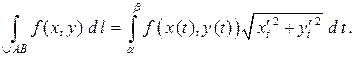 Аналогично, для пространственной кривой, заданной параметрическими уравнениями
Аналогично, для пространственной кривой, заданной параметрическими уравнениями 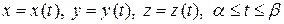 , имеем
, имеем
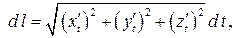
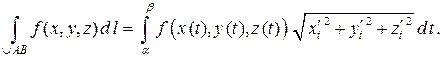
Пример 2. Найти массу верхней полуокружности радиуса 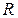 , если плотность
, если плотность 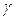 в каждой ее точке равна ординате этой точки.
в каждой ее точке равна ординате этой точки.
Решение. Масса кривой вычисляется с помощью криволинейного интеграла:

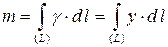 .
.
Для вычисления интеграла запишем параметрические уравнения окружности: 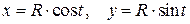 .
.
|
Параметр 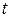 есть угол между радиус-вектором точки окружности и осью
есть угол между радиус-вектором точки окружности и осью 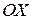 (рис. 2). Для верхней полуокружности параметр
(рис. 2). Для верхней полуокружности параметр 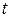 меняется от 0 до
меняется от 0 до 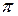 . Теперь вычислим
. Теперь вычислим 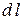 :
:
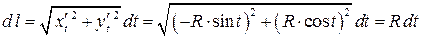 .
.
Подставим в искомый интеграл 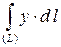 выражения для
выражения для 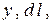 расставим пределы изменения
расставим пределы изменения 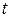 и вычислим получившийся определенный интеграл:
и вычислим получившийся определенный интеграл:
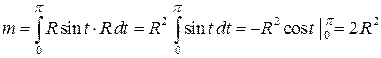 .
.
 2014-02-02
2014-02-02 6622
6622
