Двойной интеграл в прямоугольной системе

Вычисление двойного интеграла 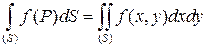сводится к вычислению двух определенных интегралов. Рассмотрим два случая.

Случай 1. Пусть область 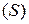в плоскости ограничена линиями 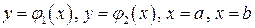(рис. 3). Тогда

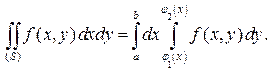
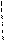
Интеграл, стоящий в правой части формулы (7.18), называют повторным или двукратным. В повторном интеграле сначала следует вычислить внутренний интеграл при фиксированном . В результате получим функцию, зависящую от переменной : 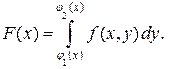Затем вычисляют внешний интеграл от функции .

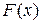Дадим нестрогое (физическое) обоснование формулы для случая неотрицательной подынтегральной функции 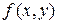. Как было установлено ранее, двойной интеграл равен массе пластины с плотностью 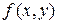. Покажем, что повторный интеграл, стоящий в правой части равенства, также равен массе пластины 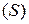. Для этого разобьем фигуру 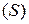на ячейки прямыми, параллельными осям координат (рис. 3). Выделим ю вертикальную полоску. В каждой ее ячейке выберем точку 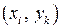так, чтобы все выбранные точки лежали на одной вертикали (рис. 3). Вычислим плотность 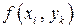в выбранной точке и массу прямоугольной ячейки

.

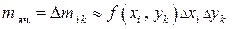Подсчитаем массу й вертикальной полоски 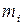, просуммировав массы ячеек 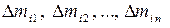и вынеся за знак суммы общий множитель :

.

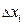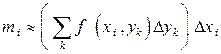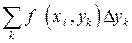Так как выбранные точки лежат на одной вертикали, то они имеют одинаковую абсциссу . Значит – фиксировано в сумме , и эта сумма является интегральной суммой для функции 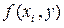по переменной 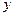, изменяющейся на отрезке 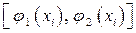(рис. 3). При малых значениях 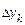интегральная сумма функции близка к интегралу от этой функции, т.е.

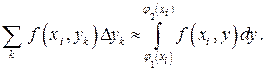
Интеграл, стоящий в правой части этого приближенного равенства, является значением выше введенной функции в точке . Поэтому для массы вертикальной полоски имеем

.

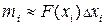Суммируя массы вертикальных полосок, получим значение массы пластины

.

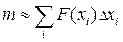Сумма 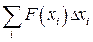является интегральной суммой функции 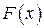по переменной 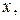изменяющейся на отрезке 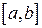. При 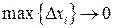эта интегральная сумма стремится к интегралу 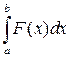. Подставляя выражение 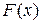через интеграл, получим

.

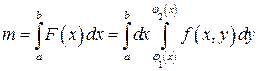Таким образом, масса пластины, с одной стороны, равна двойному интегралу из формулы, с другой стороны, равна двукратному интегралу из той же формулы. Следовательно, эти интегралы равны между собой.

Чтобы успешно пользоваться на практике формулой, рекомендуем:

1) построить область интегрирования;

2) записать двойной интеграл через повторный; в повторном интеграле сначала расставить внутренние пределы интегрирования, т.е. пределы изменения 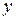. Для этого на чертеже (рис. 3) нужно двигаться параллельно оси . При этом мы войдем в фигуру через линию, на которой 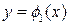, а выйдем через линию, на которой 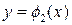, т.е. переменная интегрирования 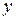меняется от 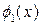до ;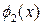

3) проецируя область 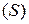на ось 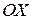, расставить внешние пределы интегрирования (это всегда – числа, а не функции);

4) вычислить внутренний интеграл при постоянном , затем – внешний интеграл.

Случай 2. Пусть область 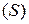в плоскости 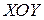(рис. 4) ограничена линиями 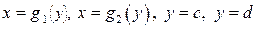. Тогда

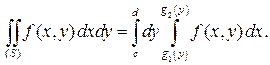
Чтобы пользоваться формулой, рекомендуем:

1) построить область интегрирования;

2) записать двойной интеграл через повторный; в повторном интеграле сначала расставить внутренние пределы интегрирования, т.е. пределы изменения . Для этого на чертеже (рис. 4) нужно двигаться параллельно оси 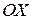. При этом войдем в фигуру через линию 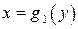, а выйдем через линию 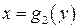, т.е. переменная интегрирования 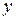меняется от 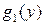до ;

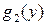3) проецируя область на ось , расставить внешние пределы интегрирования;

4) вычислить внутренний интеграл при постоянном , затем – внешний интеграл.

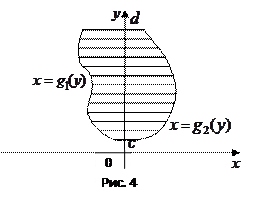Пример 1. Вычислить момент инерции относительно оси плоской фигуры, ограниченной линиями , , 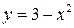если плотность .

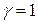Решение. Момент инерции плоской фигуры вычисляется с помощью двойного интеграла по формуле при :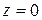

.

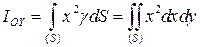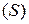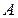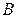Чтобы вычислить двойной интеграл, построим область (рис. 5). Найдем точки пересечения и линий 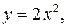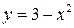. Получим 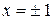, 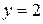. Таким образом, фигура 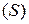ограничена снизу линией 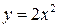, сверху – линией 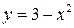, 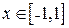. Поэтому по формуле

-1

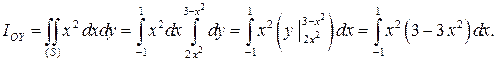Так как подынтегральная функция четная, то интеграл от нее по промежутку 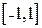равен удвоенному интегралу по промежутку 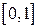. Поэтому

.

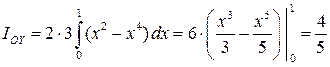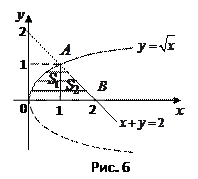Пример 7.15. Найти массу плоской фигуры, ограниченной линиями 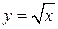, , 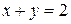, 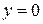если плотность .

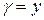Решение. Построим фигуру (рис. 6). Линия 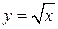есть верхняя половина параболы 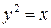, линия 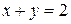– прямая. Фигура ограничена сверху двумя линиям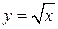и и 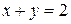. Поэтому использовать формулу нерационально: придется разбить область на две част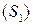и и 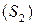, а интеграл – на сумму двух интегралов.

Удобнее воспользоваться формулой; учитывая, что слева область ограничена дугой ОА, на которой 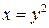, а справа ─ отрезком АВ, на котором 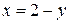, имеем:

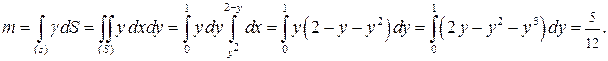
Для сравнения запишем двойной интеграл по формуле:

.

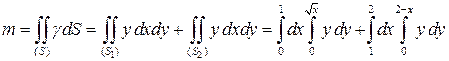Результат будет тот же, но объем вычислений – больше, так как придется вычислить два интеграла вместо одного.