Вектор 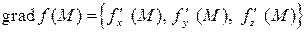 является важной характеристикой скалярного поля. Введем условный оператор
является важной характеристикой скалярного поля. Введем условный оператор 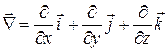 (оператор Гамильтона или вектор “набла”). С его помощью удобно записать градиент скалярного поля
(оператор Гамильтона или вектор “набла”). С его помощью удобно записать градиент скалярного поля
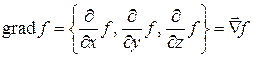 .
.
Отметим ряд свойств градиента.
1). Скалярное поле 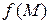 в точке
в точке 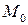 быстрее всего возрастает в направлении вектора
быстрее всего возрастает в направлении вектора 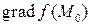 со скоростью, равной
со скоростью, равной 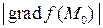 .
.
2). Скалярное поле 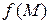 в точке
в точке 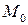 быстрее всего убывает в направлении, противоположном вектору
быстрее всего убывает в направлении, противоположном вектору 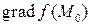 , со скоростью, равной
, со скоростью, равной 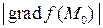 .
.
3). Вектор 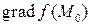 направлен по нормали к поверхности уровня поля
направлен по нормали к поверхности уровня поля 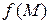 , проходящей через точку
, проходящей через точку 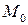 .
.
4). Дифференциальные свойства:
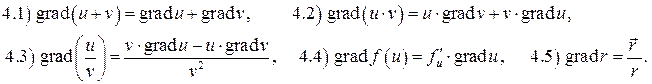
Проверим эти свойства.
1. Из формулы и определения скалярного произведения следует, что
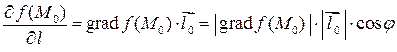 ,
,
где 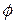 ─ угол между векторами
─ угол между векторами 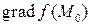 и
и 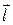 . Так как длина единичного вектора
. Так как длина единичного вектора 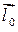 равна единице, то
равна единице, то
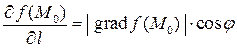 .
.
Поэтому 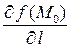 принимает наибольшее значение, равное
принимает наибольшее значение, равное 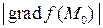 , когда
, когда 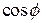 =1, то есть угол
=1, то есть угол 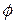 между векторами
между векторами 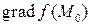 и
и 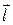 равен нулю и
равен нулю и 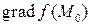
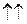
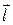 .
.
2. Производная 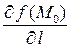 будет принимать наименьшее значение, когда
будет принимать наименьшее значение, когда 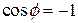 , т.е. угол
, т.е. угол 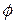 =
=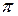 и
и 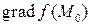
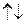
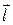 .
.
3. Поверхность уровня поля 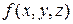 имеет уравнение
имеет уравнение 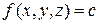 . Нормальный вектор этой поверхности
. Нормальный вектор этой поверхности 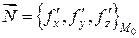 совпадает с
совпадает с 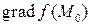 . Значит, вектор
. Значит, вектор 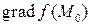 направлен по нормали к поверхности уровня поля
направлен по нормали к поверхности уровня поля 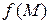 , проведенной в точке
, проведенной в точке 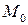 .
.
|
|
|
4.1. 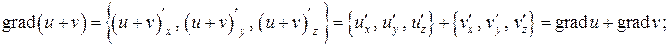
аналогично проверяются свойства 4.2), 4.3), 4.4);
для проверки свойства 4.5) учтем, что 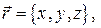
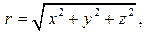
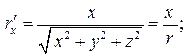 аналогично,
аналогично, 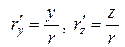 и поэтому
и поэтому
 .
.
Из первого и третьего свойств следует инвариантное определение градиента, т.е. определение, не зависящее от системы координат:
Градиент скалярного поля 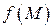 в точке
в точке 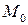 есть вектор, который
есть вектор, который
а) по величине равен наибольшей скорости возрастания поля 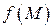 в точке
в точке 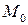 ,
,
б) направлен по нормали к поверхности уровня поля 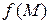 , проходящей через точку
, проходящей через точку 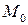 , в сторону наибольшего возрастания поля.
, в сторону наибольшего возрастания поля.
Пример 1. Найти наибольшую скорость возрастания поля 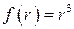 в точке
в точке 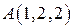 .
.
Решение. Найдем градиент поля:
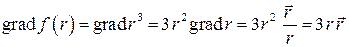 .
.
Наибольшая скорость возрастания поля в точке 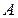 равна
равна
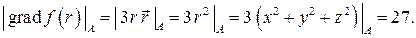
Пример 2. Доказать оптическое свойство эллипса: лучи, выходящие из одного фокуса эллипса, после отражения от эллипса проходят через другой фокус эллипса.
Решение. Пусть 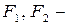 фокусы эллипса;
фокусы эллипса; 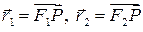 . Рассмотрим
. Рассмотрим
 скалярное поле
скалярное поле 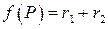 . По определению эллипса точка
. По определению эллипса точка 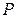 принадлежит эллипсу тогда и только тогда, когда
принадлежит эллипсу тогда и только тогда, когда 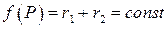 , т.е. эллипс есть линия уровня скалярного поля
, т.е. эллипс есть линия уровня скалярного поля  ; поэтому
; поэтому 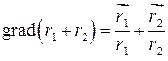 направлен по нормали к эллипсу в точке
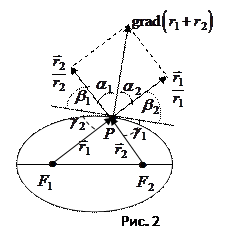
направлен по нормали к эллипсу в точке 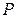 . Кроме того, этот вектор направлен по диагонали параллелограмма, построенного на векторах
. Кроме того, этот вектор направлен по диагонали параллелограмма, построенного на векторах 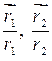 . Длины этих векторов равны единице, поэтому параллелограмм является ромбом и его диагональ является биссектрисой угла ромба, т.е.
. Длины этих векторов равны единице, поэтому параллелограмм является ромбом и его диагональ является биссектрисой угла ромба, т.е. 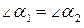 . Тогда
. Тогда 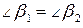 , как углы дополнительные до прямого. Так как
, как углы дополнительные до прямого. Так как 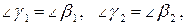 то
то 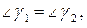 т.е. луч, выходящий из фокуса
т.е. луч, выходящий из фокуса 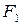 эллипса, после отражения от эллипса пройдет через другой фокус
эллипса, после отражения от эллипса пройдет через другой фокус 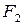 .
.
 2014-02-02
2014-02-02 8885
8885
