Пусть функция  – дифференцируема в точке
– дифференцируема в точке 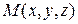 . Тогда
. Тогда
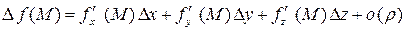 ,
,
где 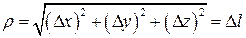 и
и 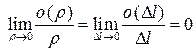 .
.
Поделим равенство (8.1) на 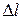 :
:
 .
.
Рассмотрим вектор 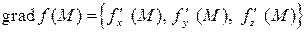 , называемый градиентом поля
, называемый градиентом поля 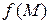 , и вектор
, и вектор 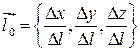 , равный единичному вектору направления
, равный единичному вектору направления 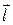 . Тогда равенство (8.2) можно записать в виде
. Тогда равенство (8.2) можно записать в виде
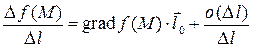 ,
,
где первое слагаемое есть скалярное произведение векторов 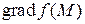 и
и 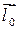 .
.
В пределе при 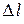 , стремящемся к нулю, получим:
, стремящемся к нулю, получим:
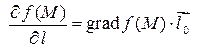 ,
,
где 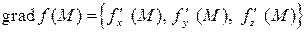 ─ градиент скалярного поля
─ градиент скалярного поля 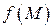 ,
, 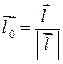 ─ единичный вектор направления
─ единичный вектор направления 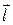 .
.
 2014-02-02
2014-02-02 1603
1603








