Оценка качества регулирования по ЛЧХ

Инженерный метод частотного анализа качества регулирования является графо-аналитическим. Он основан на использовании логарифмических частотных характеристик разомкнутой одноконтурной системы.

Аналитическая оценка качества регулирования замкнутой системы основана на сопоставлении переходных функций замкнутой системы автоматического регулирования с логарифмическими частотными характеристиками разомкнутой системы.

Принятый для анализа 3-й порядок системы автоматического регулирования позволяет установить связь между параметрами САР, характерными особенностями ЛЧХ разомкнутой системы и показателями качества регулирования, определяемыми переходной функцией замкнутой системы. Установленные применительно к системе 3-го порядка закономерности можно распространить на системы более высоких порядков, поскольку система 3-го порядка отображает динамические свойства систем автоматического регулирования любого порядка.

В зависимости от закона регулирования пропорционального или интегрального структурная схема системы 3-го порядка может иметь вид, показанный на рисунке. Динамические характеристики САР 3-го порядка с пропорциональным регулятором определяются четырьмя параметрами: общим коэффициентом усиления К ₀ и постоянными времени трех апериодических звеньев.Динамические характеристики САР третьего порядка с интегральным регулятором определяются тремя параметрами: общим коэффициентом усиления К ₀ и постоянными времени двух апериодических звеньев.

– пропорциональный закон регулирования

– интегральный закон регулирования

анализ переходных и передаточных функций замкнутых систем, а также определение признаков связи их с ЛАЧХ разомкнутой системы выполнены с целью упрощения для САР с интегральным законом регулирования. Полученные результаты могут быть применены для САР с пропорциональным законом регулирования.

Анализ динамических характеристик сделан на основе переходных и передаточных функций замкнутой системы по задающему q ×1(t)и возмущающему z ×1(t)воздействиям.

Положение ЛАЧХ исследуемой разомкнутой системы в координатных осях определяется ординатой общего коэффициента усиления 20×lg К ₀ и частотами сопряжения 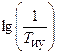, 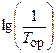характеристик апериодических звеньев с существенными постоянными времени, в данном случае исполнительного устройства Т _иу и объекта регулирования Т _ор. В исследовании принято соотношение Т _иу > Т _ор.

Оценка качества регулирования основана на сопоставлении ординат точек перелома линеаризованной ЛАЧХ разомкнутой системы при частотах сопряжения наклонных отрезков характеристик апериодических звеньев САР, а также частоты среза ЛАЧХ с приведенными параметрами передаточных функций замкнутых систем автоматического регулирования.

Качество регулирования считают удовлетворительным, если изменение выходной переменной y (t)при возмущающем воздействии z ×1(t)носит апериодический или мало-колебательный характер. Качество регулирования при неизменных величинах постоянных времени звеньев системы зависит только от общего коэффициента усиления К ₀.

Главная передаточная функция разомкнутой системы 3-го порядка:

– с интегральным регулятором

,

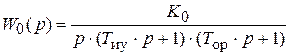– пропорциональным регулятором

.

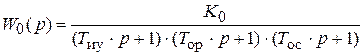Здесь К ₀ – общий коэффициент усиления системы.

Апериодический характер переходного процесса выходной переменной при возмущающем воздействии в системе 3-го порядка с интегральным законом регулирования возможен в пределах изменения общего коэффициента усиления системы 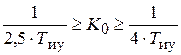и соотношении постоянных времени .

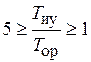Логарифмическая амплитудно-частотная характеристика разомкнутой САР определяется выражением:

.

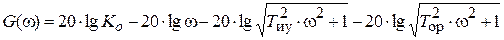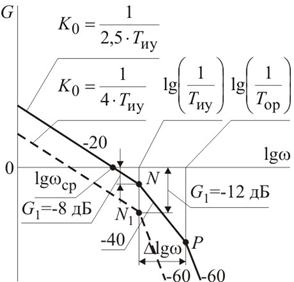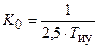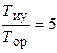Графики логарифмических амплитудно-частотных характеристик, с указанным пределам изменения общего коэффициента усиления К ₀ и соотношениями постоянных времени для апериодического процесса показаны на рисунке. На графике, выделенном сплошной линией для и , ордината точки N сопряжения ЛАЧХ с отрезком NP, увеличивающим наклон до –40 дБ/дек при частоте 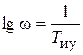, составляет G ₁ = –8 дБ. Разность абсцисс точек сопряжения N и P отрезка NP при соотношении постоянных времени 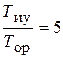составляет .

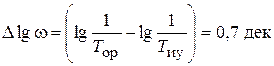Частота среза ЛАЧХ определяет запас устойчивости по фазе .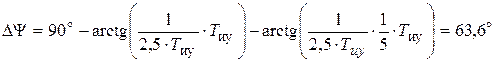

При равенстве постоянных времени Т _иу = Т _ор наклон отрезка NP составляет –60 дБ/дек. График ЛАЧХ выделен штриховой линией. Ордината точки сопряжения N при общем коэффициенте усиления системы 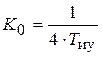равна G ₁» – 12 дБ.

Частота среза ЛАЧХ 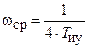определяет запас устойчивости по фазе .

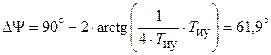Оценку времени регулирования замкнутой системы производят на основе сопоставления переходной функции приведенного колебательного звена и частоты среза ЛАЧХ w_cp приближенной формулой:

.

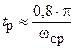Мало-колебательный характер со степенью колебательности μ = 2 переходного процесса выходной переменной при возмущающем воздействии в системе 3-го порядка с интегральным законом регулирования возможен в пределах изменения общего коэффициента усиления системы 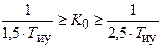и соотношении постоянных времени .

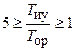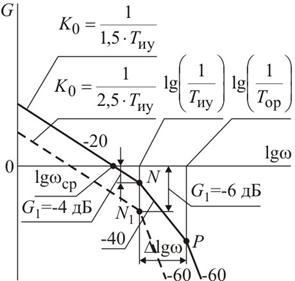
Графики логарифмических амплитудно-частотных характеристик, соответствующих указанным пределам коэффициента усиления системы К ₀ и соотношениям постоянных времени показаны на рисунке. На графике, выделенном для 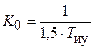и 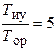сплошной линией, ордината точки N сопряжения ЛАЧХ с отрезком NP, увеличивающим наклон до –40 дБ/дек, составляет G ₁ = –4 дБ.

Частота среза ЛАЧХ 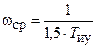определяет запас устойчивости по фазе .

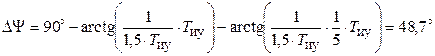При равенстве постоянных времени Т _иу = Т _ор наклон отрезка NP составляет –60 дБ/дек. График ЛАЧХ выделен штриховой линией. Ордината точки сопряжения N при общем коэффициенте усиления системы 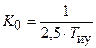составляет G ₁» – 8 дБ.

Частота среза ЛАЧХ 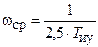определяет запас устойчивости по фазе .

Оценку времени регулирования замкнутой системы производят звена по частоте среза ЛАЧХ w_cp приближенной формулой:

.

Степень колебательности переходного процесса выходной переменной возрастает до μ = 3 при общем коэффициенте усиления системы 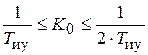и соотношении постоянных времени 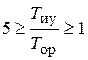. Ордината точки N изменения наклона ЛАЧХ до –40 дБ/дек при и 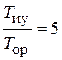составляет G ₁ = 0 дБ. Частота среза ЛАЧХ , запас устойчивости по фазе.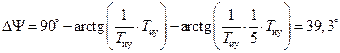

При 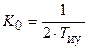и Т _иу = Т _ор ордината точки N изменения наклона до –60 дБ/дек составляет G ₁ = –6 дБ. Частота среза ЛАЧХ определяет запас устойчивости по фазе .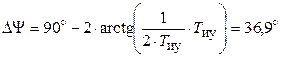

Оценку времени регулирования замкнутой системы производят по частоте среза ЛАЧХ 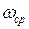приближенной формулой:

.

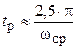Правила оценки качества регулирования.

1. Процесс регулирования может быть апериодическим или мало-колебательным, если наклон ЛАЧХ при частоте среза не превышает –20 дБ/дек. При большей крутизне наклона следует ожидать колебательный процесс регулирования.

2. Для обеспечения апериодического процесса регулирования точка сопряжения отрезка, увеличивающего наклон ЛАЧХ правее частоты среза до –40 дБ/дек, должна быть расположена ниже оси частот на 8…10 дБ, для обеспечения мало-колебательного процесса – на 4…6 дБ.

3. Дополнительно для обеспечения апериодического и мало-колебательного процессов разность абсцисс Dlgw точек сопряжения отрезка, увеличивающего наклон ЛАЧХ правее частоты среза до –40 дБ/дек, должна быть более 0,3 дек, или отношение постоянных времени, соответствующих этим частотам сопряжения, должно быть не менее двух. Если это условие не выполняется, то ожидается усиление колебательности переходного процесса.

4. Для обеспечения удовлетворительного качества САУ с интегральными законами регулирования запас устойчивости по фазе должен быть:

- при апериодическом процессе ∆ψ ≥ 60°;

- при мало-колебательном процессе со степенью колебательности μ = 2 ∆ψ ≥ 50°;

- при мало-колебательном процесса со степенью колебательности μ = 3 ∆ψ ≥ 40°.

5. Для обеспечения удовлетворительного качества САУ с пропорциональными законами регулирования запас устойчивости по фазе должен быть:

- при апериодическом процессе ∆ψ ≥ 70°;

- при мало-колебательном процессе со степенью колебательности μ = 2 ∆ψ ≥ 60°;

- при мало-колебательном процесса со степенью колебательности μ = 3 ∆ψ ≥ 40°.

6. Время регулирования можно оценить приближенной формулой для:

- апериодического переходного процесса: ;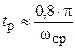

- мало-колебательного процесса при μ = 2: ;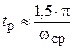

- мало-колебательного процесса при μ = 3: .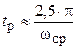

7. Для обеспечения апериодического или мало-колебательного процесса регулирования при недостаточной разности абсцисс Dlgw точек сопряжения отрезка, увеличивающего наклон ЛАЧХ правее частоты среза до –40 дБ/дек, или отношения соответствующих этим частотам сопряжения постоянных времени менее 2, надо уменьшить общий коэффициент усиления системы в 1,5…2 раза. Это соответствует смещению ЛАЧХ на 3…6 дБ вниз относительно оси абсцисс.