3.1. Частотный критерий устойчивости Найквиста.
Критерий устойчивости, основанный на использовании частотных характеристик, был разработан в 1932 г. американским инженером-исследователем Г.Найквистом применительно к устройствам радиотехники. В 1938 г. российский ученый А.В.Михайлов обобщил этот критерий и применил его для исследования устойчивости замкнутых систем автоматического управления, используя амплитудно-фазовую характеристику разомкнутой системы.
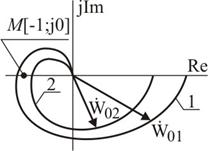
Формулировка критерия Найквиста: для устойчивости замкнутых систем, устойчивых в разомкнутом состоянии достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы при изменении угловой частоты w от 0 до ¥ не охватывала точку М с координатами [–1;j0] на комплексной плоскости. На рисунке АФХ, соответствующая вектору 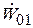 , является неустойчивой, а АФХ, соответствующая вектору
, является неустойчивой, а АФХ, соответствующая вектору 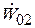 – устойчивой.
– устойчивой.
 Физический смысл критерия применительно к устойчивым в разомкнутом состоянии системам можно пояснить, рассмотрев изменение амплитуды А и фазы Y гармонического сигнала при его прохождении последовательно через все n звеньев разомкнутой системы.
Физический смысл критерия применительно к устойчивым в разомкнутом состоянии системам можно пояснить, рассмотрев изменение амплитуды А и фазы Y гармонического сигнала при его прохождении последовательно через все n звеньев разомкнутой системы.
|
|
|
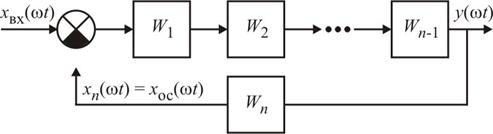 |
Гармонический сигнал на входе системы x вх(w t) = A вх×sinw t, на выходе обратной связи (звено с номером n) разомкнутой системы xn (w t) = An ×sin(w t + Y n). Если установить частоту w гармонических сигналов такой, что фаза сигнала xn (w t) на выходе главной обратной связи разомкнутой системы Y n = –180°, то отношение амплитуд А n/ А вх гармонических сигналов x вх(w t) и xn (w t) будет характеризовать ослабление или усиление мощности гармоничного сигнала при его прохождении по контуру обратной связи до места её замыкания.
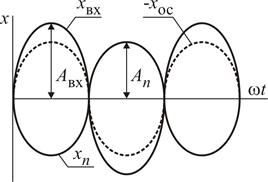 При замыкании главной отрицательной обратной связи фаза гармонического сигнала xn (w t) инвертируется устройством сравнения, то есть сдвигается на 180°. В результате, фаза сигнала обратной связи по отношению к входному сигналу становится равной Y n = 360° или Y n = 0, следовательно, входной сигнал и сигнал обратной связи совпадут по фазе. На рисунке инвертированный сигнал обратной связи показан штриховой линией. Таким образом, обратная связь замкнутой системы при фазовом сдвиге сигналов Y n = –180° становится положительной.
При замыкании главной отрицательной обратной связи фаза гармонического сигнала xn (w t) инвертируется устройством сравнения, то есть сдвигается на 180°. В результате, фаза сигнала обратной связи по отношению к входному сигналу становится равной Y n = 360° или Y n = 0, следовательно, входной сигнал и сигнал обратной связи совпадут по фазе. На рисунке инвертированный сигнал обратной связи показан штриховой линией. Таким образом, обратная связь замкнутой системы при фазовом сдвиге сигналов Y n = –180° становится положительной.
Известно, что любой усилитель с положительной обратной связью переходит в релейный режим, то есть теряет устойчивость и переходит в режим ограничения максимального уровня выходного сигнала, если коэффициент усиления по контуру обратной связи равен или больше единицы. Если коэффициент усиления по контуру положительный обратной связи будет меньше 1, то усилитель устойчиво функционирует в режиме усиления. Отношение амплитуды гармонического сигнала Аn на выходе звена обратной связи к амплитуде А вх входного сигнала характеризует его усиление по контуру главной обратной связи. С другой стороны это отношение равно модулю вектора частотной функции разомкнутой системы
|
|
|
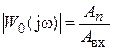 .
.
 Следовательно, если АФХ разомкнутой системы не охватывает точку М с координатами (–1;j0), то модуль вектора частотной функции разомкнутой системы при фазе Y0 = –180° будет
Следовательно, если АФХ разомкнутой системы не охватывает точку М с координатами (–1;j0), то модуль вектора частотной функции разомкнутой системы при фазе Y0 = –180° будет 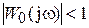 , а замкнутая система – устойчива. В том случае, когда АФХ разомкнутой системы охватывает точку с координатами (–1;j0), модуль вектора частотной функции разомкнутой системы при фазе Y0 = –180° будет
, а замкнутая система – устойчива. В том случае, когда АФХ разомкнутой системы охватывает точку с координатами (–1;j0), модуль вектора частотной функции разомкнутой системы при фазе Y0 = –180° будет 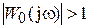 , а замкнутая система – неустойчива.
, а замкнутая система – неустойчива.
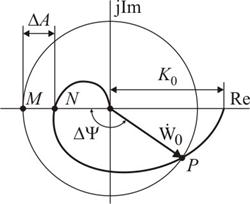
Критерий устойчивости Найквиста позволяет оценить запасы устойчивости замкнутой системы по модулю и фазе. Запас устойчивости по модулю D А равен отношению разности амплитуд гармонического сигнала на входе и выходе разомкнутой системы к амплитуде входного сигнала при фазе Y0 = –180°:
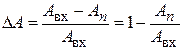 .
.
На амплитудно-фазовой характеристике эта величина представлена отрезком МN от точки М (–1; j0) до точки N пересечения АФХ разомкнутой системы с вещественной осью:
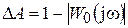 .
.
Запас устойчивости по фазе DY можно определить по разности фаз Y n гармонических сигналов входного x вх(w t) и на выходе разомкнутой системы xn (w t), при условии что их амплитуды равны Аn = А вх. На АФХ разомкнутой системы, устойчивой в замкнутом состоянии, запас по фазе определяют углом между отрицательной частью вещественной оси и вектором частотной функции 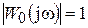 , проведенным из начала координат в точку P пересечения АФХ с окружностью радиусом 1. Модуль вектора частотной функции разомкнутой системы в этом случае равен
, проведенным из начала координат в точку P пересечения АФХ с окружностью радиусом 1. Модуль вектора частотной функции разомкнутой системы в этом случае равен 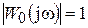 , а фазаY0 отличается от –180° на величину DY угла запаса по фазе:
, а фазаY0 отличается от –180° на величину DY угла запаса по фазе:
DY = 180 – Y0.
Запасы устойчивости по модулю и фазе взаимосвязаны с качеством регулирования САУ. При уменьшении запасов качество регулирования ухудшается, при увеличении запасов – улучшается. Поэтому нормы запасов задают интервалами DА ³ 0,5…0,8; DY ³ 30…60°.
Основные достоинства критерия устойчивости Найквиста:
1. Возможность оценки устойчивости замкнутой системы по АФХ разомкнутой системы.
2. Возможность определения АФХ разомкнутой системы или отдельных её звеньев экспериментальным путем.
3. Возможность количественной оценки запасов устойчивости по модулю и фазе.
Существенным недостатком критерия устойчивости Найквиста является большой объем вычислительной и графической работы при расчете и построении АФХ. Этот недостаток легко устранить, применив для оценки устойчивости логарифмические частотные характеристики.
3 .2. Оценка устойчивости систем автоматического управления по ЛЧХ с использованием критерия Найквиста.
Метод оценки устойчивости по логарифмическим частотным характеристикам представляет собой, по сути, рассмотренный в предыдущем разделе критерий устойчивости Найквиста, перенесенный с амплитудно-фазовой характеристики на логарифмические частотные характеристики разомкнутой системы.
Из сопоставления АФХ и ЛЧХ следует, что пересечение АФХ окружности с центром в начале координат на комплексной плоскости радиусом 1 соответствует пересечению ЛАЧХ с осью абсцисс, так как lg1 = 0. Частоту, при которой модуль вектора частотной функции разомкнутой системы равен 1, называют частотной среза ЛАЧХ wср разомкнутой системы. Точке М пересечения АФХ с отрицательной частью вещественной оси соответствует фаза Y0 = –180°, следовательно, ЛФЧХ при этом пересекают уровень –180°.
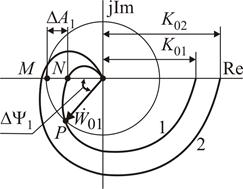 Амплитудно-фазовые характеристики, показанные на рисунке, соответствуют системе автоматического управления, в структурной схеме которой либо отсутствует форсирующие звенья, либо они не оказывают заметного влияния на вид АФХ. В такой САУ повышение общего коэффициента усиления К 0 разомкнутой системы может привести к потере устойчивости. На рисунке показана АФХ при двух значениях коэффициента усиления К 01 и К 02. Согласно критерию Найквиста система автоматического управления с общим коэффициентом усиления К 01 устойчива (кривая 1), так как её АФХ не охватывает точку М (–1, j0); при К 02 САУ неустойчива (кривая 2).
Амплитудно-фазовые характеристики, показанные на рисунке, соответствуют системе автоматического управления, в структурной схеме которой либо отсутствует форсирующие звенья, либо они не оказывают заметного влияния на вид АФХ. В такой САУ повышение общего коэффициента усиления К 0 разомкнутой системы может привести к потере устойчивости. На рисунке показана АФХ при двух значениях коэффициента усиления К 01 и К 02. Согласно критерию Найквиста система автоматического управления с общим коэффициентом усиления К 01 устойчива (кривая 1), так как её АФХ не охватывает точку М (–1, j0); при К 02 САУ неустойчива (кривая 2).
|
|
|
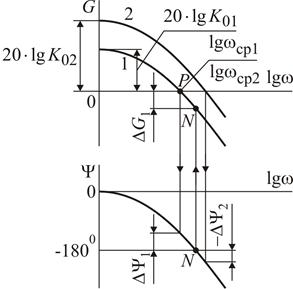 Логарифмические частотные характеристики, соответствующие АФХ приведены на рисунке. Из рисунка следует, что при повышении общего коэффициента усиления от К 01 до К 02 частота среза wср смещается вправо по оси абсцисс до значения wср2, а запас устойчивости по фазе при неизменной фазо-частотной характеристике из положительного DY1становится отрицательным –DY2, то есть ЛФЧХ переходит уровень –180°. Замкнутая система в этом случае становится неустойчивой.
Логарифмические частотные характеристики, соответствующие АФХ приведены на рисунке. Из рисунка следует, что при повышении общего коэффициента усиления от К 01 до К 02 частота среза wср смещается вправо по оси абсцисс до значения wср2, а запас устойчивости по фазе при неизменной фазо-частотной характеристике из положительного DY1становится отрицательным –DY2, то есть ЛФЧХ переходит уровень –180°. Замкнутая система в этом случае становится неустойчивой.
Формулировка критерия устойчивости Найквиста применительно к ЛЧХ: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если при всех положительных значениях ЛАЧХ разомкнутой системы, её ЛФЧХ расположена выше уровня –180°.
Запас устойчивости по фазе DY на ЛФЧХ определяют в виде разности уровня –180° и фазе Y0 при частоте среза ЛАЧХ:
DY = 180 – Y0(wср).
Запас устойчивости по модулю, определяемый отрезком D А при пересечении АФХ с отрицательной частью вещественной оси, на ЛАЧХ соответствует ординате D G при частоте пересечения ЛФЧХ уровня –180°. Запасу устойчивости по модулю D А ≥ 0,5 соответствует абсолютное значение ординаты ЛАЧХ: 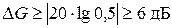 .
.
 2014-02-02
2014-02-02 3687
3687
