Последовательное соединение звеньев. Передаточные функции систем

Передаточные функции систем

Метод анализа структурной схемы

Заданы: структурная схема, входная и выходная величины системы. Ставиться задача определить передаточную функцию системы.

Для определения передаточной функции системы воспользуемся методом обратного движения. Метод обратного движения позволяет получить операторное уравнение, из которого и составляется передаточная функция. Заключается он в следующем.

Начинают с выходной величины системы. Двигаясь по схеме против направления передачи сигнала, связывают выходную величину, ближайшую передаточную функцию и ее входной сигнал операторным уравнением. Затем, продолжая двигаться против направления входного сигнала, достигают вторую передаточную функцию. Составляют операторное уравнение, в котором выходной сигнал будет равен произведению второй передаточной функции на следующий входной сигнал. Исключая промежуточную величину, связывают выходную величину системы и очередной входной сигнал. Повторяя процедуру, получают связь выходной величины системы с входной величиной системы.

Сумматоры дают два направления и по каждому надо двигаться против передачи сигнала.

В итоге получается операторное уравнение, которое содержит все передаточные функции, регулируемую величину и регулирующую величину. Из операторного уравнения находят передаточную функцию всей системы.

Применяя метод, соблюдают принцип суперпозиции, по которому два сигнала, проходящих по каналу, не взаимодействуют между собой. Их можно сложить и пропустить через звено, или сначала пропустить, а потом сложить - результат будет один и тот же. То есть

(Х ₁ + Х ₂) К = Х К = К Х ₁ + К Х ₂ = Y

Рассмотрим систему из трех последовательно соединенных звеньев с передаточными функциями К ₁, К ₂, К ₃, рис. 4.1.

Y

Х 3

Х 2

Х 1

К ₁ К ₂ К ₃

Рис. 4.1. Схема последовательного соединения звеньев

Входная величина системы Х ₁, выходная Y. Передаточные функции К ₁, К ₂, К ₃ считаются известными. Надо найти передаточную функцию системы W = Y / Х ₁.

Применяя метод обратных движений, выразим Y, X₃, X₂ через К ₃, К ₂, К ₁ и последовательно исключим промежуточные сигналы.

Y = K ₃ X ₃ = K ₃ K ₂ X ₂ = K ₃ K ₂ K ₁ X ₁.

Следовательно,

W = K ₁ K ₂ K ₃.

Нетрудно вывести для любого числа последовательно соединенных звеньев передаточную функцию системы

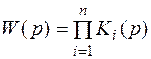(4.1)

Если какие то группы звеньев соединены заранее, можно найти их передаточные функции W_i и затем соединить последовательно. Структура формулы для определения передаточной функции системы не измениться:

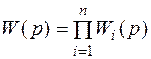(4.2)