Рассмотрим схему из трех параллельно соединенных звеньев с передаточными функциями К 1, К 2, К 3, рис. 4.2.
 Х Y 1
Х Y 1


 К 1
К 1
 Х Х Y 2 Y
Х Х Y 2 Y




 К 2
К 2
 |
 Х Y 3
Х Y 3
 К 3
К 3
Рис. 4.2. Схема параллельного соединения звеньев.
Каждое i -звено имеет одинаковый входной сигнал Х и разные выходные сигналы Yi. Все входные сигналы звеньев равны входному сигналу системы Х. Выходной сигнал системы равен сумме выходных сигналов звеньев: Y = Y 1 + Y 2 + Y 3. Передаточные функции К 1, К 2, К 3 считаются известными. Надо найти передаточную функцию системы W = Y / X.
Записываем:
Y = Y 1 + Y 2 + Y 3 = K1 X + K2 X + K 3 X = (К 1 + К 2 + К 3) X.
W = К 1 + К 2 + К 3 .
Не представляет труда вывести для любого числа параллельно соединенных звеньев передаточную функцию системы:
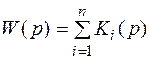 . (4.3)
. (4.3)
Если параллельно соединяются не звенья, а их соединения в группы с передаточными функциями Wi, то в формулу (4.3) войдут передаточные функции Wi:
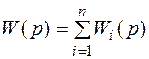 . (4.4)
. (4.4)
Пропорционально-интегральный регулятор получают параллельным соединением двух звеньев, уравнения которых
y = kx и 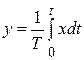 .
.
Найти передаточную функцию системы.
Составим операторные уравнения (предварительно продифференцировав второе уравнение, чтобы избавиться от интеграла):
Y (p) = k X (p), 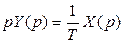 .
.
Запишем передаточные функции звеньев:
K 1(p) = k, 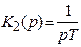
и, следуя формуле (4.3.), получим:
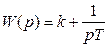 .
.
Пропорционально-дифференциальный регулятор образуется параллельным соединением усилительного и идеального дифференцирующего звеньев.
Найти передаточную функцию и дифференциальное уравнение системы.
Запишем передаточные функции звеньев,
K 1(p) = k, K 2(p) = Tp
и согласно формуле (4.3.) получим:
W (p) = k + Tp.
Операторное уравнение
Y (p) = (k + Tp) X (p)
показывает, что дифференциальным уравнением регулятора будет
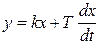 .
.
 2014-02-02
2014-02-02 1269
1269
