Система с обратной связью

Чтобы получить систему с обратной связью, надо соединить звенья параллельно, но с противоположным движением сигналов, как показано на рис. 4.3.

U (p) – сигнал от задающего устройства, в данном случае – входной сигнал системы. С – сумматор. E (p) – ошибка слежения, входной сигнал звена с передаточной функцией К (р). Y ₁(p) – выходной сигнал звена К (р), который одновременно является выходным сигналом системы Y (p). Линия, по которой передается входной сигнал системы, называется линией (каналом) прямой связи. Линия, начинающаяся от точки разветвления R и передающая сигнал в обратном направлении, называется линией (каналом) обратной связи. Сумматор, звено К (р) расположены на линии прямой связи. Звено К _ос(р) включено в линию обратной связи.

Рис. 4.3. Схема соединения с обратной связью.

Система с обратной связью называется замкнутой.

Если сигнал линии обратной связи входит в сумматор со знаком, противоположным знаку задающего сигнала U (p), обратная связь называется отрицательной. Это указывается зачернением соответствующего сектора сумматора или пометкой знаком «минус». Примем, что обратная связь отрицательная, E (p) = U (p) – Y _oc(p). (в случае положительной обратной связи E (p) = U (p) + Y _oc(p)).

Для замкнутой системы можно составить несколько передаточных функций.

4.2.4. Передаточная функция разомкнутой системы. Получается, если разорвать обратную связь, например возле сумматора, как показано волнистыми черточками на рис. 4.3. В таком случае выходным сигналом оказывается Y _oc(p), а передаточная функция будет отношением Y _oc(p) к U (p):

W = 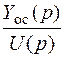(4.5)

Методом обратного движения осуществим построение операторного уравнения разомкнутой системы (аргумент р опустим):

Y _oc = K _oc Y = K _oc K E = K _oc K U

По определению (4.5), передаточной функцией разомкнутой системы будет:

W (p) = K _oc(p) K (p). (4.6)

Если вместо звена К (р) будет соединение звеньев с передаточной функцией W ₁(p), вид формулы остается тем же:

W (p) = K _oc(p) W ₁(p). (4.7)

Передаточная функция разомкнутой системы характеризует собственные динамические свойства системы.

4.2.5. Передаточная функция замкнутой системы. Выходным сигналом, как обозначено на схеме рис. 4.3, будет Y (p), входным U (p).

Передаточная функция замкнутой системы – обозначим ее - есть отношение изображения регулируемой величины к изображению задающего воздействия:

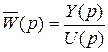. (4.8)

Двигаясь по контуру регулирования против направления передачи сигнала, получаем:

Y = Y ₁ = K E = K (U – Y _oc) = K U – K K _oc Y.

Y (1 + K K _ос) = K U.

По определению (4.8) передаточной функцией замкнутой системы будет:

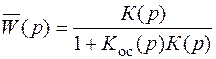. (4.9)

Знак «плюс» в знаменателе соответствует отрицательной обратной связи. В случае положительной обратной связи ставиться знак «минус».

Обратная связь через усилительное звено называется жесткой, через дифференцирующее звено – мягкой.

Если в линии обратной связи звено отсутствует, и выходной сигнал системы непосредственно подается на вход, тогда К _ос(р) = 1. Замкнутая система имеет передаточную функцию

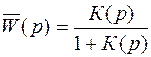. (4.10)

Передаточная функция замкнутой системы характеризует передачу системой задающего воздействия, его воспроизведение регулируемой величиной.