Пример 4.6

Разомкнутую систему из последовательно соединенных двух одинаковых инерционных звеньев замыкают. Найти передаточную функцию.

По условию, K ₁(p) = K ₂(p) = k / (Tp + 1). Значит, передаточная функция разомкнутой системы

.

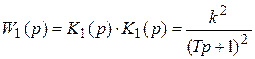Согласно формуле (4.5), передаточная функция замкнутой системы

.

Пример 4.7.

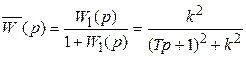Интегрирующее звено соединяется последовательно с инерционным звеном. Соединение охватывается жесткой отрицательной обратной связью.

Найти передаточную функцию.

Передаточные функции звеньев:

, , .

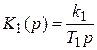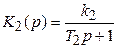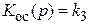Перемножая K ₁(p) и K ₂(p), получаем передаточную функцию соединения:

.

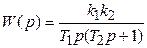Передаточная функция замкнутой системы

.

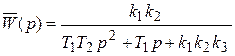Если произведение k ₁ k ₂ k ₃ вынести за скобку, обозначить T ₁ T ₂/ k ₁ k ₂ k ₃ = T ²,

T ₁/ k ₁ k ₂ k ₃ = T ₀ и 1/ k ₃ = k, проявится структура передаточной функции звена второго порядка:

.

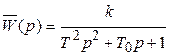То есть, замкнутая система будет вести себя либо как колебательное звено (при условии T ₀ < 2 T), либо как апериодическое звено (при условии T ₀ > 2 T).

Пример 4.8.

Инерционное звено последовательно соединяется с интегрирующем. К цепочке параллельно подсоединяется звено с единичной передаточной функцией. Вся система охватывается жесткой обратной связью.

Найти передаточную функцию системы.

Структурная схема представлена на рис. 4.4.

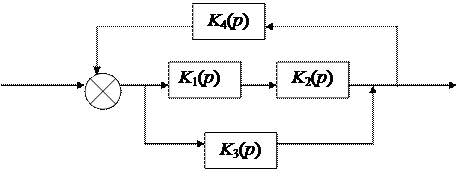Рис. 4.4.

Выпишем передаточные функции:

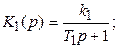
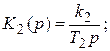K ₃(p) = 1; K ₄(p) = k ₄.

Находим передаточную функцию разомкнутой системы из двух звеньев, K ₁(p) и K ₂(p):

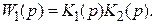
Находим передаточную функцию параллельного соединения:

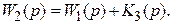
Находим передаточную функцию замкнутой системы с учетом того, что обратная связь положительная:

.

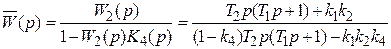Можно убедиться, что результат будет таким же, если нанести на схему обозначения сигналов и применить метод обратного движения.