Конспект лекций 9 страница

2. Ток – упорядоченное движение заряженных частиц. Сила Ампера есть суммарный результат действия магнитного поля на всю совокупность носителей тока, следовательно, магнитное поле оказывает силовое воздействие на движущуюся в нем заряженную частицу. Оно выражается силой Лоренца:

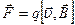(9.4.4)

Ее величина

F=qυB sin α (9.4.5)

Здесь q – заряд частицы, движущейся со скоростью – υ в магнитном поле B под углом – α к силовой линии.

Отметим, что , так что сила Лоренца сообщает частице нормальное ускорение, изменяя направление, но не величину скорости. Сила Лоренца не совершает механическую работу и не изменяет кинетическую энергию частицы. Пусть частица массы т с зарядом q влетает со скоростью υ в однородное магнитное поле B поперек его силовых линий. Рассчитаем ее траекторию (рис. 51). Силовые линии перпендику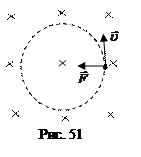лярны плоскости рисунка и изображены крестиками, они входят в плоскость рисунка. F=qυB=ma_n=mu ²/ R. Частица равномерно движется по окружности радиуса 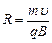. Ее период обращения 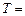2p R / u = 2p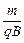, круговая частота w =. Если заряд влетает под углом к силовым линиям, то его движение целесообразно разделить на два: вдоль и поперек силовых линий. В продольном по отношению к полю направлении на частицу не действует сила, и она движется равномерно и прямолинейно. В поперечном направлении частица движется по окружности, в итоге ее траектория будет спиралью, «накрученной» на силовые линии.

Рассмотренное действие магнитного поля на движущиеся электрические заряды наблюдается в явлениях природы (радиационные пояса планет, северное сияние) и используется в науке и в технике (ускорители заряженных частиц, масс-спектрометры, МГД-генераторы, магнитные линзы в различных электронных устройствах).

3. Пусть в однородном магнитном поле находится плоский прямоугольный контур с током. На рис. 52 указаны оси декартовых координат. Силовые линии магнитного поля параллельны оси y. Ток в контуре течет в направлении 12341. Стороны 12 и 34 длиной а, стороны 23 и 41 длиной в. Нормаль к контуру параллельна плоскости xy и образует с силовыми линиями (осью у) угол a. На каждую сторону контура действуют силы Ампера, их векторы показаны на рисунке. Силы F ₂₃ и F₄₁ лежат в плоскости контура. Их действие компенсируется жесткостью контура. Силы F ₁₂ = F ₃₄ = IBв параллельны оси х. Они 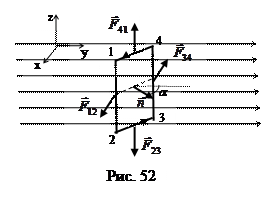образуют пару сил с плечом asina и стремятся повернуть контур так, чтобы его плоскость стала перпендикулярна силовым линиям. Момент этой пары сил M=IBaвsina, и вектор направлен по оси z. Произведение силы тока I на площадь контура S=ав называют магнитным моментом контура с током:

p_m=IS (9.4.6)

Магнитный момент контура с током является вектором, направленным по нормали к контуру: . Магнитный момент контура – это представление контура с током в виде магнитной стрелки.Отметим, что направление тока в контуре и нормаль к нему связаны правилом правого винта. Вращающий момент равен векторному произведению магнитного момента контура и магнитной индукции внешнего магнитного поля:

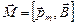(9.4.7)

Его модуль

M=p_mBsina (9.4.8)

Если контур находится в неоднородном магнитном поле, то, помимо вращающего момента, на него могут действовать дополнительные силы, втягивающие его в поле или выталкивающие из него. Действие магнитного поля на контур с током находит широкое практическое применение, например, в электроизмерительных приборах (амперметрах, вольтметрах и т.п.)

4. Силы, действующие на проводники и контуры с током в магнитном поле, могут их перемещать и совершать механическую работу. Рассмотрим плоский прямоугольный 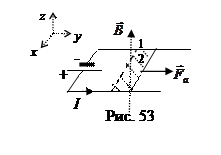контур с постоянным током в однородном магнитном поле (рис. 53). Пусть плоскость контура перпендикулярна силовым линиям, одна его сторона подвижная (вспомните лекционную демонстрацию «Станок Ампера»). На правую сторону рамки, длина которой l, действует сила Ампера F_a=IBl и перемещает ее из положения 1 в положение 2 на расстояние dy. Работа силы dA= F_ady =IBldy. Учитывая, что Bldy=BdS=dФ [36], получили формулу работы в магнитном поле

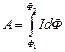(9.4.9)

При неизменной силе тока

A=I (Ф ₂ -Ф ₁)= I D Ф (9.4.10).

Итак, работа в магнитном поле происходит при перемещении проводника или контура с током, если

изменяется сцепленный с контуром магнитный поток.

§ 9.5. Магнитное поле в веществе

1. Все тела состоят из атомов, в которых движутся электроны и протоны и создают собственное магнитное поле. Внешнее магнитное поле влияет на их движение. Поэтому все вещества являются магнетиками – они намагничиваются и создают собственное магнитное поле . В веществе это поле складывается с внешним магнитным полем (в вакууме) 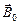, так что

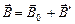(9.5.1)

Изменение поля в веществе по сравнению с полем в вакууме характеризует относительная магнитная проницаемость m - безразмерная величина. Ее физический смысл аналогичен диэлектрической проницаемости. Она показывает, во сколько раз поле в веществе изменяется по сравнению с полем в вакууме:

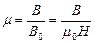(9.5.2)

Опыт показывает, что в намагниченности вещества определяющую роль играют электроны атомов. Орбитальное движение электрона можно рассматривать как миниатюрный круговой ток, обладающий собственным магнитным моментом. Помимо орбитальных магнитных моментов электроны обладают еще специфически квантовой характеристикой – спиновым магнитным моментом. Сумма орбитальных и спиновых магнитных моментов электронов атома определяет магнитные свойства вещества.

2. По магнитным свойствам вещество делится на три группы: диамагнетики, парамагнетики и ферромагнетики. Первые две группы являются слабомагнитными, они создают очень слабое собственное поле, для них m отличается от единицы в третьем-четвертом знаке после запятой и не зависит от внешнего поля. Для технически важных слабых магнетиков значения магнитной проницаемости представлены в соответствующих таблицах физических величин.

Диамагнетики намагничиваются против внешнего поля, так что внесение диамагнетика во внешнее магнитное поле ослабляет его. К диамагнетикам относятся инертные газы, водород, вода, висмут, серебро и другие. Диамагнетики выталкиваются внешним магнитным полем. Удлиненные диамагнитные тела (стержни) ориентируются поперек силовых линий. Для диамагнетиков m £ 1.

Парамагнетики намагничиваются по полю и усиливают его. Парамагнетики втягиваются во внешнее магнитное поле, удлиненные парамагнитные тела вытягиваются вдоль силовых линий. Примером парамагнетиков являются воздух, платина, алюминий, жидкий кислород. Для парамагнетиков m ³ 1.

Третья группа – ферромагнетики – сильномагнитные материалы. Они получили свое название от железа. Ферромагнетиками являются такие химически чистые вещества: железо, никель, кобальт, гадолиний, а также многочисленные сплавы, в том числе и не содержащие указанные вещества. Магнитная проницаемость ферромагнетиков значительно больше единицы и зависит от величины внешнего поля. Способность ферромагнетиков значительно усиливать магнитное поле (на 3-5 порядков) широко используются в технике. В ферромагнетиках наблюдается явление гистерезиса. Гистерезис (от греческого – отставание, запаздывание) проявляется в том, что в одном и том же внешнем магнитном поле намагниченность ферромагнетика зависит от его предыстории и принимает одно из возможных значений из целого диапазона. После снятия внешнего магнитного поля в ферромагнетике сохраняется остаточная намагниченность. Именно это свойство проявляется в постоянных магнитах.

В итоге рассмотрения отметим, что полученные нами ранее формулы для магнитного поля в вакууме пригодны для магнитного поля в веществе, если в них заменить m ₀ на m ₀ m. Напомним, что с аналогичным способом описания поля в веществе мы уже познакомились в электростатике

§ 10.1. Основной закон электромагнитной индукции

1. Проводник с током создает магнитное поле. Оказывается, и обратное верно: при определенных условиях магнитное поле создает (индуцирует) в проводнике электрический ток. Это и есть явление электромагнитной индукции, открытое в 1831 г. М.Фарадеем: при вдвигании в замкнутую проволочную катушку постоянного магнита или при выдвигании его из катушки по катушке шел ток, причем, его направление изменялось как при изменении направления движения магнита, так и при изменении его полярности. Аналогичный результат получался, если постоянный магнит заменить электромагнитом, а также, если на неподвижный магнит надевать замкнутую катушку или снимать ее с него. Из этих и подобных им опытов был сделан вывод, что при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ток. Такой ток получил название индукционного. Направленное движение зарядов в проводнике создается электродвижущей силой, так что при изменении сцепленного с контуром магнитного потока контур берет на себя роль источника тока. Возникающая в нем электродвижущая сила называется ЭДС индукции e _и. На основании опытов Ленц сформулировал правило, которое устанавливает направление индукционного тока и носит его имя: индукционный ток имеет такое направление, чтобы препятствовать причине своего возникновения. Это значит, что магнитное поле индукционного тока препятствует изменению внешнего магнитного потока, создающего индукционный ток. Математическое выражение этого явления называется основным законом электромагнитной индукции и имеет вид:

e _и= (10.1.1)

Знак «минус» в формуле (10.1.1) есть выражение правила Ленца. Если контур представляет собой катушку из последовательно соединенных одинаковых витков, то такая ЭДС возникнет в каждом витке, и на концах катушки из N штук витков она составит e _и= N. Полный магнитный поток, сцепленный со всеми витками катушки, называют потокосцеплением

Y=NФ (10.1.2)

Для многосвязного контура, каким является катушка,

e _и= (10.1.3)

2. Причиной изменения магнитного потока и возникновения в контуре ЭДС индукции может быть изменение со временем магнитного поля, площади контура или его ориентации в пространстве. Рассмотрим примеры технического применения явления электромагнитной индукции.

Пример 1. Пусть контур площадью S расположен в однородном магнитном поле поперек силовых линий. С контуром сцеплен магнитный поток Ф₁=BS. При изменении потокав контуре возникает ЭДС, и в замкнутой цепи (ее сопротивление R), куда входит рассматриваемый контур, течет ток силой 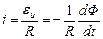и переносит заряд dq=idt. За время изменения магнитного потока пройдет заряд q=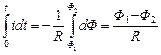. Если Ф₂ =0, то q =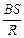. Такой принцип действия используется в приборах для измерения магнитной индукции. При резком удалении датчика из магнитного поля (или при повороте его в поле на 180⁰, когда магнитный поток изменяется вдвое) отклонение стрелки указывает величину магнитной индукции.

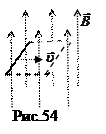
Пример 2. В однородном магнитном поле движется поперек силовых линий прямолинейный проводник длиной l (рис. 54). При своем движении он пересекает магнитный поток dФ=BdS=Bludt, так что e _и= Вlu.. На концах проводника скапливаются разноименные электрические заряды, создающее электростатическое поле с напряженностью Е=e _и/ l. Заметим, что, согласно правилу Ленца, на ближнем к нам конце окажется положительный заряд, а на дальнем – отрицательный. Подобное явление наблюдается на крыльях самолетов, так как в полете они пересекают силовые линии магнитного поля Земли. Для стекания этих зарядов на концах крыльев расположены металлические щеточки.

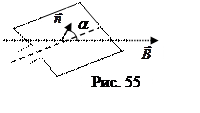Пример 3. В однородном магнитном поле равномерно вращается с угловой скоростью w плоская прямоугольная рамка площадью S.. Ось вращения лежит в плоскости рамки и перпендикулярна силовым линиям (рис. 55). Нормаль к рамке образует с силовыми линиями угол a = w t. Рамку пронизывает поток Ф=ВS cos a= ВS cos w t, так что

e _и= ВSw sin w t. Рассмотренная рамка – модель генератора переменного тока. Если к ней присоединить нагрузку, то в цепи потечет переменный ток.

§ 10.2. Самоиндукция и взаимная индукция

1. Протекающий по контуру ток создает в окружающем пространстве магнитное поле и сцепляет с контуром магнитный поток (потокосцепление) Y. Его величина пропорциональна магнитной индукции, а, следовательно, силе тока в контуре, так как В ~ I. Коэффициент пропорциональности называется индуктивностью контура, обозначается L, в СИ измеряется в генри (Гн). По определению

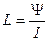(10.2.1)

Покажем на примере соленоида, что индуктивность зависит от геометрии контура (его формы и размеров), а также от магнитных свойств окружающей среды: Ψ=ФN=BSN. В соленоиде B=μ ₀ μIn=μ ₀ μIN / l. В результате получили формулу индуктивности соленоида:

L=μ ₀ μN ² S/l=μ ₀ μn ² lS= μ ₀ μn ² V (10.2.2)

Здесь V - объем соленоида.

2. Явление электромагнитной индукции возникает при изменении сцепленного с контуром магнитного потока независимо от причины, вызвавшей это изменение, в том числе, при изменении силы тока в самом контуре. Явление возникновения в контуре ЭДС индукции при изменении тока в нем называется самоиндукцией. Основной закон электромагнитной индукции для контура с постоянной индуктивностью примет вид:

e_s= (10.2.3)

Здесь индекс «s» показывает, что речь ведется об ЭДС самоиндукции, созданной изменением тока в контуре. Формула (10.2.3) указывает, что ЭДС самоиндукции пропорциональна скорости изменения силы тока и препятствует ее изменению. Рассмотрим цепь, содержащую источник постоянного тока с ЭДС e, сопротивление R,индуктивность L и ключ К (рис. 56). Пусть в исходном состоянии ключ находится в положении 1, и по цепи течет ток I ₀ = . Отключим источник постоянного тока переводом ключа в положение 2 (будем считать, что цепь при этом все время оставалась замкнутой). В новой цепи источника тока нет, и ток должен обратиться в ноль. Вследствие явления самоиндукции ток в цепи обладает «инерционностью»: его изменению препятствует ЭДС самоиндукции. Запишем закон Ома для этой новой цепи: iR=e_s=. Решив дифференциальное уравнение с разделяющимися переменными: 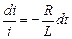, получаем: 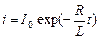, т.е. сила тока экспоненциально стремится к нулю. При подключении к первоначально разомкнутой цепи источника постоянного тока (в начальный момент времени ключ приводят в положение 1) явление самоиндукции препятствует мгновенному достижению током установившегося значения I ₀. Сила тока экспоненциально растет: 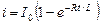. Скорость изменения тока при замыкании и размыкании цепи тем меньше, чем больше индуктивность контура. Это явление имеет ясный физический смысл: противодействие ЭДС самоиндукции причине своего возникновения. Если контур находится в ферромагнитной среде (соленоид с ферромагнитным сердечником), то при замыкании и размыкании цепи e_s может значительно превосходить значение e. При размыкании цепи e_s, приложенная к месту разрыва цепи, может оказаться столь велика, что воздушный зазор «пробивается» газовым разрядом и возникает электрическая дуга. Для ее гашения в сильноточных цепях используют специальные меры безопасности. Такая дуга может быть полезной, например, для сварки и резки металлов. В электро- и радиотехнике используют дроссели – катушки с ферромагнитным сердечником, имеющие большую индуктивность. Дроссель оказывает большое сопротивление быстропеременным токам. Их используют, например, для подавления радиопомех.

3. Если два проводящих контура находятся так близко друг от друга, что ток, текущий в одном из контуров (например, I ₁ в первом), создает магнитный поток в другом контуре (Y ₂₁ во втором). Коэффициент пропорциональности между ними зависит от геометрии контуров и их взаимного расположения. Он называется взаимной индуктивностью L ₂₁:

Y ₂₁= L ₂₁ I ₁ (10.2.4)

Такие контуры называются связанными. При изменении тока в одном из связанных контуров в нем возникает ЭДС самоиндукции. Одновременно в другом контуре также возникает явление электромагнитной индукции, оно называется взаимной индукцией. ЭДС взаимной индукции

e _вз2=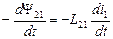 (10.2.5)

Здесь L ₂₁=const, в контурах нет ферромагнетиков. Аналогично, если изменяется ток во втором контуре, в первом возникает ЭДС взаимной индукции. Ее величина зависит от L ₁₂ , и не обязательно L ₂₁= L ₁₂.

Явление взаимной индукции широко используется в технике. Например, электрические трансформаторы, повышающие и понижающие напряжение переменного тока – обязательные устройства в линиях электропередач.

§ 10.3. Энергия магнитного поля

1. Вновь вернемся к электрической цепи, изображенной на рис. 56. Пусть ключ находился в положении 1. Переведем его в положение 2, отключив внешний источник постоянного тока. Ток, поддерживаемый ЭДС самоиндукции, экспоненциально убывает. Найдем работу тока за время убывания его от I ₀ до нуля:

A=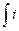e_sdt=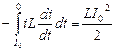. После исчезновения тока в соленоиде исчезло магнитное поле. Закономерен вывод, что источником работы тока была энергия магнитного поля соленоида. Магнитное поле контура с током имеет энергию:

(10.3.1)

2. Поле в соленоиде занимает весь объем, и его энергия равномерно распределена по объему, так как поле однородное. Используя формулы (9.3.4) и (10.2.2) для поля в соленоиде и его индуктивности, найдем: w=W/V = B ²/(2 m ₀). Полученный результат справедлив для любого магнитного поля. Если поле в данной точке известно, т.е. известны его характеристики B=mm ₀ H, то вблизи этой точки объемная плотность энергии магнитного поля [37]

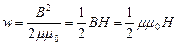(10.3.2)

§ 10.4. Вихревое электрическое поле. Уравнения Максвелла

1. Рассмотрим физический механизм явления электромагнитной индукции. На движущиеся электрические заряды магнитное поле действует силой Лоренца. В неподвижном проводнике носители тока движутся хаотически, так что действующая на них сила Лоренца хаотически меняет направление и не может упорядочить их движение. Обратимся к примеру 2, рассмотренному в § 10.1. Проводник движется поперек силовых линий, и вместе с ним движутся в одном направлении носители тока. Применяя правило левой руки, видим, что теперь на каждый носитель тока действует дополнительная сила Лоренца, направленная вдоль проводника. Она смещает разноименные заряды к противоположным концам проводника. В этом случае сторонняя сила, создающая ЭДС индукции, имеет магнитное происхождение. Посмотрим на эту ситуацию глазами наблюдателя, «сидящего» на проводнике. Относительно него проводник неподвижен, а вот магнитное поле движется. В соответствии с принципом относительности этот наблюдатель обнаружит, что произошло разделение разноименных зарядов, они сконцентрировались на противоположных концах проводника. Теперь сила Лоренца не может объяснить данный феномен. Остается предположить, что «движущееся» магнитное поле создало в проводнике дополнительное электрическое поле, которое «разделило» заряды. Если проводник замкнуть, то по нему потечет ток, созданный ЭДС индукции. Траектории зарядов будут замкнутыми, следовательно, силовые линии этого электрического поля тоже замкнутые. Таким свойством обладают вихревые поля. Переменное магнитное поле создает вихревое электрическое поле. Оно создается в пространстве, где имеется изменяющееся со временем магнитное поле. Проводник, в котором это поле создает ЭДС индукции, не нужен для возникновения вихревого электрического поля, он только регистрирует факт наличия вихревого электрического поля. Из формул (8.3.5) и (10.1.1) следует, что ЭДС индукции есть циркуляция вихревого электрического поля:

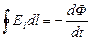(10.4.1)

2. Из явления электромагнитной индукции следует, что электрическое и магнитное поля взаимосвязаны друг с другом, и что в природе существует единое электромагнитное поле. Этот вывод был сделан Максвеллом, создателем теории электромагнитного поля. Максвелл предположил, что не только переменное магнитное поле служит источником вихревого электрического поля, но и переменное электрическое поле, подобно движущимся электрическим зарядам, создает магнитное поле. Это переменное электрическое поле Максвелл назвал током смещения. Ток смещения

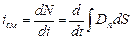(10.4.2)

Напомним, что D=ee ₀ E - электрическое смещение или электрическая индукция, вспомогательная характеристика электрического поля. N – поток вектора электрического смещения через поверхность. С учетом тока смещения теорема о циркуляции магнитной индукции (см. формулу 9.3.3) принимает вид:

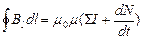(10.4.3)

3. Идея Максвелла о токе смещения «симметрична» его идее о вихревом электрическом поле: переменное электрическое поле является источником магнитного поля, переменное магнитное поле является источником электрического поля. В 1860 -1865 г.г. Максвелл разработал теорию электромагнитного поля. Ее выражением является система уравнений Максвелла:

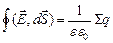(10.4.4)

(10.4.5)

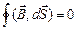(10.4.6)

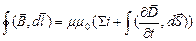(10.4.7)

Эти уравнения записаны в векторной форме, знак «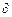» обозначает частную производную и подчеркивает изменение соответствующего поля не в пространстве, а во времени. Смысл этих уравнений мы уже обсудили. Рассмотренные нами электростатическое и магнитостатическое поля – частные случаи электромагнитного поля, и они тоже удовлетворяют уравнениям Максвелла, Вы легко убедитесь в этом самостоятельно.

Теория Максвелла завершила создание классической электродинамики. Ее компактные уравнения включают в себя все знания о классических (неквантовых) электромагнитных полях. Она теоретически предсказала существование электромагнитных волн, опередив их открытие. В основе современной электротехники, радиотехники и электронной техники лежат уравнения Максвелла. В XIV в. английский философ Уильям Оккам установил, что чем более мы приближаемся к истине, тем проще оказываются основные законы. Этот опытный факт получил название «бритвы Оккама». Применительно к науке он утверждает, что по мере развития науки число основных законов уменьшается. Теория Максвелла, да и вся физика являются блестящей иллюстрацией к «бритве Оккама».

Автор благодарит всех, изучивших представленный материал и просит указать опечатки, неточности, а также недостаточно ясно изложенные места для внесения корректив.

[1] Номер формулы состоит из трех частей: первые две – номер параграфа, третья – порядковый номер формулы в этом параграфе. Номер параграфа содержит два числа: первое – номер главы, второе – порядковый номер параграфа главы.

[2] Только для таких малых углов можно применять векторные операции, например, векторное сложение по правилу параллелограмма. Для больших углов это правило не действует.

[3] В пределах этого объема еще не проявляется дискретность атомного строения вещества, но он достаточно мал, чтобы можно было считать, что свойства вещества одинаковые во всех его точках.

[4] Здесь F_^= ||, так будем впредь обозначать модуль проекции на плоскость, перпендикулярную оси вращения, вектора силы, приложенной к телу.

[5] Напоминаем, что есть разные способы записи векторного произведения: квадратные скобки или знак умножения -´.

[6] 1 а.е.м.= 1/12 массы атома углерода»1,66^.10^-27 кг

[7] Даже если ln N= 10, то N= 2,7¹⁰ > 1000, соответственно, 2,7²⁰>1000000=10⁶

[8] Феномен (ударение на втором слоге) – явление (греч.)

[9] Чуть позже о термине «идеального»

[10] Нормальными называют такие условия: давление р= 760 мм рт.ст = 10⁵ Па (нормальное атмосферное давление), температура Т =273 К (0⁰ С)

[11] В нашем случае N ® ¥ означает, что мы рассматриваем макротело (термодинамическую систему), определение которому дали в § 5.1.

[12] Вспомните, что такое по определению средняя арифметическая и средняя квадратичная скорости и постарайтесь увидеть соответствие этих формул определениям.

[13] Убедитесь в этом самостоятельно на материале §5.2.

[14] Приборы, принцип действия которых основан на этой формуле – альтиметры – используются в авиации для определения высоты полета.

[15] Его называют эффективным диаметром, так как молекулы на самом деле не являются твердыми шариками. В этой модели молекулы разных газов имеют разные эффективные диаметры порядка 10^-9м.

[16] Напомним, что термодинамические диаграммы - это графики, на осях координат которых откладываются два из трех параметров состояния газа, например, p и V, p и T, V и T.

[17] Q_V означает, что тепло передают так, что объем газа не изменяется, на это указывает индекс V.