Определение. ДУ 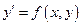 наз-ся однород-м, если ф-я
наз-ся однород-м, если ф-я  может быть представлена, как ф-я отнош-я своих аргументов
может быть представлена, как ф-я отнош-я своих аргументов 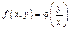
Пример. 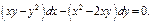
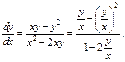
Ф-я 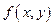 наз-ся однородной ф-й измерения
наз-ся однородной ф-й измерения 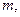 если
если 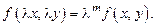
Примеры: 1) 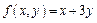 - 1-й порядок однородности.
- 1-й порядок однородности. 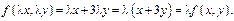
2) 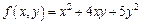 - 2-й порядок однородности.
- 2-й порядок однородности. 
3) 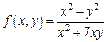 - нулевой порядок однородности (просто однородная ф-я).
- нулевой порядок однородности (просто однородная ф-я). 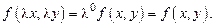
Пример приведения ф-ии. 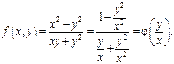
Введем вспомог-ую ф-ю 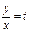 или
или 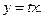 ДУ
ДУ 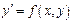 , где
, где 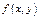 - однородная ф-я нулевого измерения, можно преобразовать к ур-ю с разделяющимися перем-ми. Действ-но
- однородная ф-я нулевого измерения, можно преобразовать к ур-ю с разделяющимися перем-ми. Действ-но 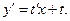 Тогда
Тогда 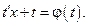
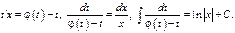
Вычислив интеграл, и перейдя к 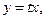 получим
получим 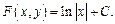 Предполагается, что
Предполагается, что 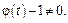 Если
Если 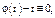 то
то 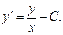
Если ур-е однородное, то подстановка tпреобразует ур-е в ур-е с разделяющимися переем-ми
 2014-02-02
2014-02-02 351
351








