Определение. Если левая часть ур-я 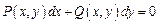 явл-ся полным диф-лом некот-й ф-и
явл-ся полным диф-лом некот-й ф-и 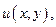 то это ур-е наз-ся ДУ в полных диф-лах.
то это ур-е наз-ся ДУ в полных диф-лах.
Это выполняется, если 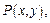
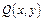 и их частные производные непрерывны в односвязной области и
и их частные производные непрерывны в односвязной области и 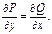
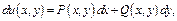
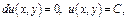
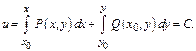
Примеры. 1) 
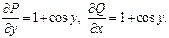


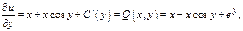
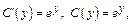
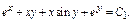
2) 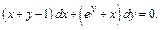
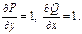
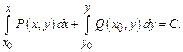 Положим
Положим 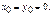
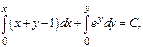
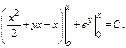
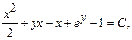
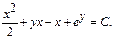
Интегрирующий множитель.
Если 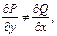 то вводят интегрирующий множитель
то вводят интегрирующий множитель 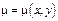 такой, что
такой, что 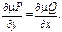
1) Если 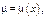 то
то 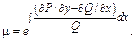
2) Если 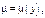 то
то 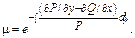
Пример. 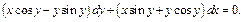
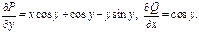
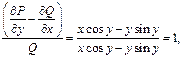
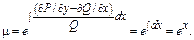
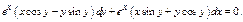
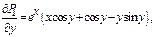
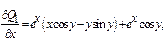
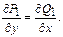
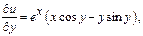
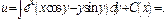
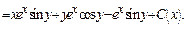
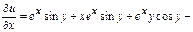
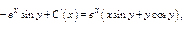
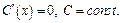
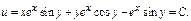
 2014-02-02
2014-02-02 402
402








