Линейные ДУ.
Определение. ДУ вида 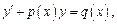 т.е. линейное относ-но неизвестной ф-ции
т.е. линейное относ-но неизвестной ф-ции  и ее производной
и ее производной 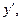 наз-ся линейным.
наз-ся линейным.
Для реш-я такого типа ур-й рассмотрим два метода: метод Лагранжа и метод Бернулли.
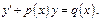 Рассмотрим однородное ДУ
Рассмотрим однородное ДУ 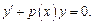 Это ур-е с разделяющимися переем-ми
Это ур-е с разделяющимися переем-ми 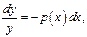
 Решение ур-я
Решение ур-я 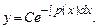 Общее реш-е неоднородного линейного ДУ имеет такой же вид, но
Общее реш-е неоднородного линейного ДУ имеет такой же вид, но 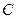 считается ф-ей
считается ф-ей 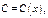 т.е.
т.е. 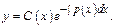 Найдем производную
Найдем производную 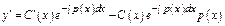 и подставим в исходное ур-е
и подставим в исходное ур-е  и
и 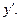
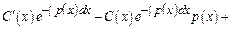
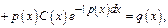
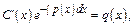
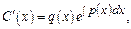
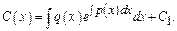 Общее реш-е линейного ДУ 1-го порядка имеет вид
Общее реш-е линейного ДУ 1-го порядка имеет вид 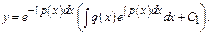
Метод Бернулли (метод замены переменной). 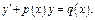
Представим неизвестную ф-ю как произвед-е 2-х ф-й 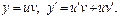 Подставим в исходное ур-е
Подставим в исходное ур-е  и
и 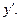 Получим
Получим 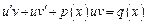 или
или 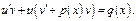 Потребуем, чтобы ф-я
Потребуем, чтобы ф-я 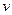 была такой, что выражение
была такой, что выражение 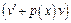 тождественно равнялось 0. Тогда исходное ур-е сводится к 2-м ур-ям с разделяющ-ся переем-ми
тождественно равнялось 0. Тогда исходное ур-е сводится к 2-м ур-ям с разделяющ-ся переем-ми 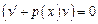 и
и 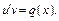 Решим их последов-но.
Решим их последов-но.
1) 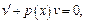
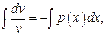
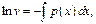
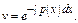
2) 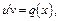
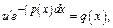
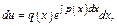

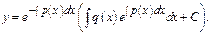
Уравнение Бернулли. 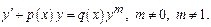
Пример. 1) Метод Лагранжа: 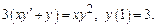
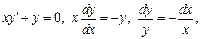
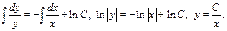
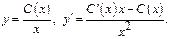
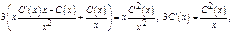

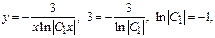
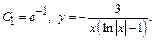
2) Метод Бернули: 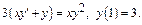
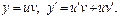
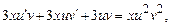
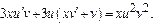
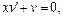
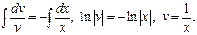
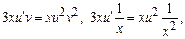
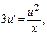
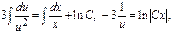
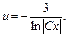
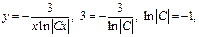

 2014-02-02
2014-02-02 645
645








