Линейно независимые системы ф-й

Линейные ДУ -го порядка.

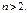
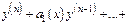
Выше изложенное переносится на ДУ порядка 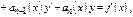(**) где 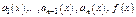- непрерывные ф-и.

Сначала рассмотрим однородное ур-е

(***)

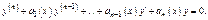Рассмотрим с-му ф-й 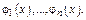Линейной комбинацией их будет 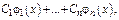где 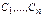- постоянные.

Определение. С-ма ф-й 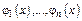наз-ся линейно независимой, если ни одну из этих ф-й нельзя представить в виде линейной комбинации остальных.

Т.е. не может быть равенства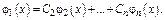

В частности 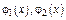линейно независимы, если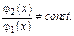

Если 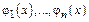не есть линейно незав-е ф-и, то они линейно зависимы.

Пример.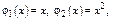

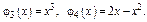
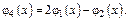
Теорема. Если 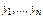суть 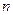частных линейно незав-х реш-й ДУ (***), то общим реш-м этого ур-я будет (****)

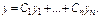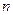Если - линейно зависимые реш-я, то, по крайней мере, одно из них выразится через остальные и ф-я будет зависеть не от , а от 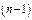произвольных постоянных. Она не даст общего реш-я ДУ.

Усл-е линейной незав-сти частных реш-й ДУ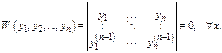

Если заданы нач-е усл-я 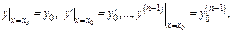то, чтобы из общего реш-я получить частное реш-е, надо решить с-му алгебр-х ур-й

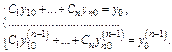
Здесь 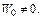Нулевым нач-м усл-м соответствует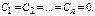

Линейно незав-ые реш-я ДУ 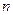- го порядка образуют фундаментальную систему решений.

Общее реш-е неоднородного ДУ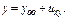

Теорема. Если 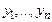- фундаментальная система реш-й ДУ то реш-м ДУ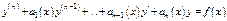явл-ся ф-я 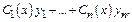где 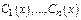удовлетворяют системе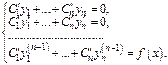

Определитель с-мы есть определитель Вронского.