Понятие с-мы ДУ. Нормальная форма. Задача Коши для с-мы. Геом-ий смысл реш-я. Линейные с-мы: вид общего реш-я. Метод исключения. Матричное представление систем ДУ
Сущ-ют процессы, где одной ф-и недостаточно для описания процесса. Далее 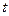 - независимая переменная;
- независимая переменная; 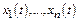 (или
(или 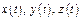 если ф-й не больше трех) - неизвестные ф-ии.
если ф-й не больше трех) - неизвестные ф-ии.
Определение. С-ой ДУ наз-ют совокупность ур-й, в каждое из которых входят незав-е переменные, искомые ф-и и их производные.
Примеры. 1)  2)
2) 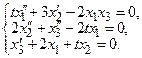
Реш-ем с-мы ДУ наз-ют совокупность ф-й 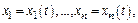 которая при подстановке в ур-я превращает их в тождества.
которая при подстановке в ур-я превращает их в тождества.
Определение. Норм-й с-й ДУ наз-ся с-ма ур-й вида 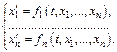
Многие с-мы ДУ можно привести к норм-й с-ме.
Пример. 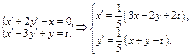
Некоторые с-мы ДУ нельзя привести к нормальной системе. Их рассматривать не будем.
Пример. 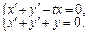
С-ма ДУ, содержащая производные высших порядков, может быть приведена к нормальной системе.
Пример. 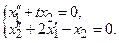 Введем дополн-ые ф-и
Введем дополн-ые ф-и 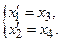 Тогда
Тогда 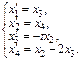
Одно ДУ 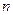 - го порядка может быть сведено к нормальной системе ДУ.
- го порядка может быть сведено к нормальной системе ДУ.
Пример. 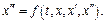
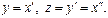
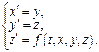
Норм-я с-ма ДУ, обычно, может быть заменена одним ДУ, порядок которого = числу ур-й с-мы.
Пример 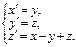
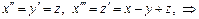
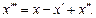
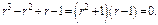
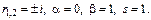
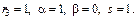
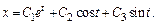
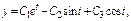
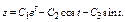
Обратный случай, когда с-ма ДУ не может быть сведена к одному ДУ.
Пример 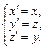 Первое ур-е не зависит от остальных.
Первое ур-е не зависит от остальных. 
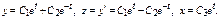
Теорема. Общее реш-е нормальной с-мы ДУ 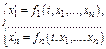 имеет вид
имеет вид 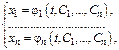 где
где 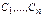 - произвольные постоянные.
- произвольные постоянные.
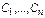 могут входить не во все ур-я.
могут входить не во все ур-я.
Задание нач-х усл-й 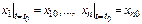 дает частное реш-е с-мы ДУ
дает частное реш-е с-мы ДУ 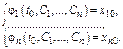
Теорема. Если правые части нормальной с-мы ДУ непрерывны вместе со своими частными производными в окрестности значений 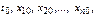 то в достаточно малом интервале
то в достаточно малом интервале 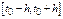 сущ-ет единств-я с-ма ф-ий
сущ-ет единств-я с-ма ф-ий 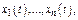 являющаяся реш-м с-мы и удовлетворяющая нач-м усл-м.
являющаяся реш-м с-мы и удовлетворяющая нач-м усл-м.
Однородная с-ма линейных ДУ
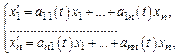
где 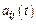 - непрерывные ф-ии.
- непрерывные ф-ии.
1) Если известно частное реш-е с-мы линейных ДУ 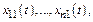 то
то 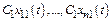 тоже является реш-м с-мы, где
тоже является реш-м с-мы, где 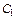 - произвольная постоянная.
- произвольная постоянная.
2) Если известны два частных реш-я с-мы линейных ДУ 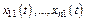 и
и 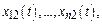 то
то 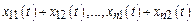 тоже явл-ся реш-ем с-мы.
тоже явл-ся реш-ем с-мы.
3) Если известны 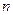 частных реш-й с-мы
частных реш-й с-мы 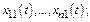 …;
…; 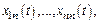 то
то 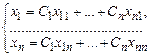 (*)
(*)
тоже является реш-ем с-мы линейных ДУ.
Совокупность реш-й образует фундаментальную с-му реш-й. Реш-е (*) явл-ся общим реш-ем однородной с-мы линейных ДУ.
Общее реш-е неоднородной с-мы линейных ДУ 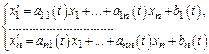
есть сумма общего реш-я однородной с-мы и частного реш-я неоднородной с-мы.
При заданных нач-х усл-х 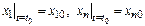 можно получить частное реш-е с-мы линейных ДУ. Для этого необходимо подставить нач-е усл-я в общее реш-е с-мы (*). Получим алгебраическую с-му ур-й
можно получить частное реш-е с-мы линейных ДУ. Для этого необходимо подставить нач-е усл-я в общее реш-е с-мы (*). Получим алгебраическую с-му ур-й 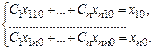
Решая с-му, получим частное реш-е с-мы линейных ДУ. Для того, чтобы с-ма алгебраических ур-й имела единственное реш-е, необходимо, чтобы определитель 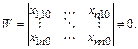
 2014-02-02
2014-02-02 341
341








