Рассмотрим однородную с-му линейных ДУ 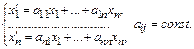
С-му можно свести к одному ДУ 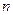 - го порядка. Будем искать частные реш-я в виде
- го порядка. Будем искать частные реш-я в виде 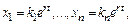 где
где 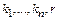 - неопределенные постоянные. Дифференцируя, получим
- неопределенные постоянные. Дифференцируя, получим 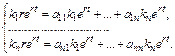
Отсюда 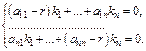
Чтобы с-ма однородных ур-й имела ненулевое реш-е, необходимо и достаточно, определитель с-мы равнялся 0 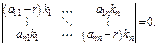
Раскрыв определитель, получим характеристическое ур-е.
Предположим, что корни действительные и простые. Рассмотрим реш-е на примере с-мы трех ур-й. Пусть корень равен 
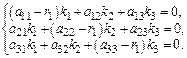
Определитель системы равен 0. Примем, что если  - простой корень, то, по крайней мере, один из миноров 2-го порядка не равен 0. Тогда одно из ур-й следует из остальных. Реш-е с-мы зависит от одной произвольной постоянной.
- простой корень, то, по крайней мере, один из миноров 2-го порядка не равен 0. Тогда одно из ур-й следует из остальных. Реш-е с-мы зависит от одной произвольной постоянной.
Пусть первые два ур-я линейно независимы. Тогда одно из реш-й будет
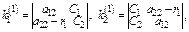
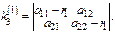
Все остальные реш-я получаются умножением чисел  на одну и ту же произвольную постоянную.
на одну и ту же произвольную постоянную.
Поступая так со всеми корнями характеристического ур-я, найдем три с-мы ф-й, каждая из которых явл-ся реш-ем с-мы линейных ДУ
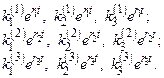
Общее реш-е с-мы линейных ДУимеет вид 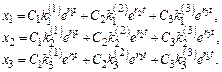
 2014-02-02
2014-02-02 332
332








