2014-02-02
350
Радикальный признак Коши.
Пусть дан ряд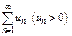 
Если сущ-ет предел 
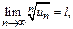то при 
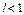- ряд сходится,
при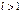 
- ряд расходится, при 
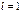- ряд может сходится или расходиться.
Пример.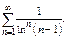 
Применим радик-й признак Коши. 
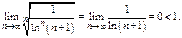Ряд сходится.
Теорема. Пусть дан ряд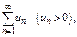 
члены которого явл-ся значениями непрерывной ф-и 
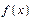при целых знач-х аргумента 
: 
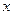и пусть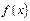 
монотонно убывает в интервале 
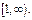Тогда ряд сходится, если сходится несобственный интеграл 
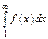и расходится, если интеграл расходится.
