Вероятность события должна удовлетворять следующим аксиомам:
 . Вероятность любого события неотрицательна:
. Вероятность любого события неотрицательна: 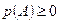 .
.
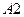 . Вероятность достоверного события равна единице:
. Вероятность достоверного события равна единице: 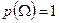 .
.
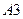 . Вероятность сумы несовместных событий равна сумме вероятностей этих событий, т.е. если
. Вероятность сумы несовместных событий равна сумме вероятностей этих событий, т.е. если 
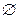 (
(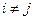 ), то:
), то: 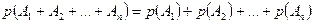 .
.
В случае произвольного, не обязательно конечного, пространства элементарных событий аксиому 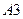 необходимо заменить более сильной, расширенной аксиомой сложения, которую нельзя вывести из аксиомы
необходимо заменить более сильной, расширенной аксиомой сложения, которую нельзя вывести из аксиомы 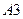 :
:
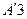 . Если имеется счетное множество несовместных событий
. Если имеется счетное множество несовместных событий 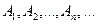 (
(
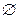 (
(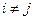 )), то:
)), то: 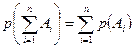 .
.
Аксиомы теории вероятностей позволяют вычислить вероятности любых событий через элементарные события. Вопрос о том, откуда берутся вероятности элементарных событий, при аксиоматическом построении теории вероятностей не рассматриваются. На практике они определяются, например, с помощью классического или статистического определения.
Из аксиом Колмогорова вытекают следующие свойства вероятности:
1. Вероятность невозможного события равна нулю 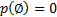 .
.
2. Сумма вероятностей противоположных событий равна единице:

3. Вероятность любого события не превосходит единицы:

4. Если событие 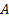 влечет за собой появление события
влечет за собой появление события 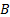 , то:
, то:
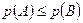
5. Если несколько событий 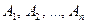 образуют полную группу событий, то:
образуют полную группу событий, то:
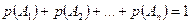 .
.
 2014-02-02
2014-02-02 5312
5312








