Геометрическая вероятность

План

РАЗЛИЧНЫЕ МЕТОДЫ РАСЧЕТА ВЕРОЯТНОСТИ СОБЫТИЙ

ЛЕКЦИЯ № 3

1. Геометрическая вероятность

2. Статистическая вероятность

3. Субъективная вероятность

4. Аксиоматическое построение теории вероятностей

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят понятие геометрической вероятности.

Понятие «геометрическая вероятность» состоит в следующем. Пусть на плоскости имеется некоторая фигура , которая содержит фигуру 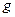. На фигуру бросается точка, которая может оказаться в любой точке фигуры G. Другими словами, в результате бросания точки (испытания) возможно бесчисленное множество исходов. В данном случае нет оснований считать неравновозможными хотя бы два каких–либо исхода из всего множества исходов. Понятно, что брошенная точка может оказаться в фигуре 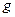, а может там и не оказаться, поэтому возможно говорить о вероятности попадания точки в фигуру 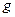. В данном случае будет естественным связать вероятность с площадями фигур 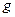и : чем больше площадь фигуры 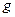, тем больше точка имеет возможностей попасть в нее. Обозначим через 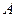событие, состоящее в попадании брошенной точки в фигуру 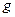, а через 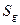и 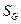– площади фигур 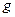и соответственно. Тогда под вероятностью события 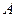будем понимать отношение данных площадей, т.е.

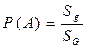(3.1)

По аналогии с понятием благоприятствующего исхода, фигуру g будем называть благоприятствующей появлению события .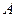

В приведенном примере рассматривались двумерные области, мерами которых были соответствующие площади. Но область может быть одномерной (кривая, прямая, отрезок), тогда ее мерой является длина. Область также может быть и трехмерной (некоторое тело в пространстве), мерой ее является объем. Исходя из этого, дадим определение геометрической вероятности.

Определение 3.1. Геометрической вероятностью события называется отношение меры области, благоприятствующей появлению события, к мере всей области.

Пример. 3.1. Задача о встрече. Двое друзей условились встретиться в определенном месте между 12 и 13 часами. Первый ждет другого 20 мин и уходит. Чему равна вероятность того, что встреча состоится?

Решение:

Обозначим моменты прихода одного из друзей через x, а другого через y. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы .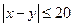

Введем систему координат. Всевозможные исходы изобразятся точками квадрата со сторонами 60; благоприятствующие встрече расположатся в заштрихованной области. Искомая вероятность равна отношению площади заштрихованной к площади всего квадрата.