Теорема2

Теорема1.

Определение4.

Функция 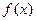называется непрерывной если бесконечно малому

приращению аргумента соответствует бесконечно малое приращение функции.

Все основные элементарные функции непрерывны в каждой точке своей области определения.

Пусть функции и 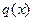непрерывны. Тогда функции 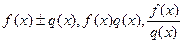также непрерывны в точке (последняя при условии, что ).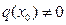

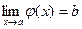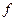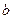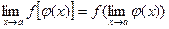Теорема3. Если и функция непрерывна в точке , то , или .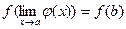

Теорема4. Пусть функция 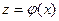непрерывна а функция 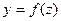непрерывна в точке 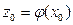. Тогда сложенная функция 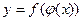непрерывна в точке .