Определение1

Свойства функций непрерывных в точке.

Функция 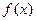называется непрерывной в точке , если предел

функции и её значение в этой точке равны, то есть.

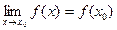(1)

Из определения следует, что если функция непрерывна

в точке , то она определена в этой точке, то есть существует .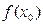

Так как, то соотношение (1) можно записать в виде

,

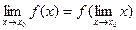то есть для непрерывной функции можно менять

местами знак функции и знак предела.

Определение2. (на языке последовательностей).

Функция называется непрерывной в точке , если для любой последовательности значений аргумента 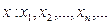сходящейся к , последовательность соответствующих значений функции: 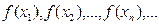сходящейся к .

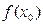Определение3. (''на языке '').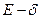

Функция 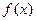называется непрерывной в точке , если для любого E>0 существует 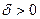такое, что для всех x удовлетворяющих неравенству

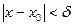, выполняется неравенство .

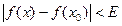Эквивалентность этих определений очевидна.

Перенесем в равенстве (1) 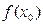в левую часть и внесём 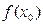под знак предела. Так как условия 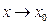и 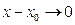равносильны, то получаем

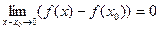(2)

Разность 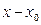называется приращением аргумента x в точке и обозначается 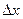, а разность 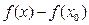- приращением функции в точке и обозначается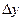. Таким образом, , .

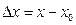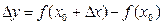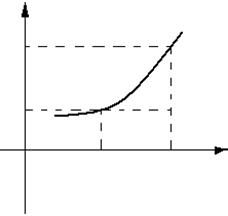
У

f (x₀+∆x) y=f(x)

∆y

f(x₀)

∆x

0 x₀ x₀+∆x x

Равенство (2) в новых обозначениях примет вид

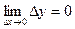(3)

Соотношение (3) является ещё одним определением непрерывности

функции в точке.