Замечание.
Теорема неверна, если отрезок 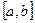 заменить интервалом
заменить интервалом 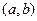 . Так, например, функция
. Так, например, функция 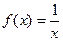 непрерывна на
непрерывна на 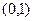 , но не ограничена, т.к.
, но не ограничена, т.к. 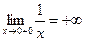 .
.
(вторая теорема Вейерштрасса о существовании наибольшего и наименьшего значения).
Если функция 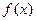 непрерывна на отрезке
непрерывна на отрезке 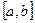 , то она принимает на этом отрезке наибольшее и наименьшее значение.
, то она принимает на этом отрезке наибольшее и наименьшее значение.
y 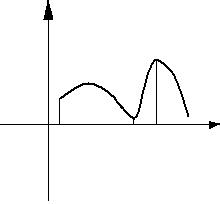
y=f(x)
M
m
0 a x1 x2 x
Теорема утверждает, что существует хотя бы одна такая точка 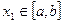 и
и 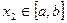 , что
, что 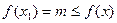 и
и 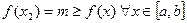 .
.
 2014-02-02
2014-02-02 455
455








