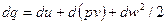
или
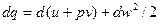
Величина в скобках (u+ pv) является энтальпией, следовательно,
dq= di + dw2/2 (**)
или, интегрируя это выражение для двух сечений:
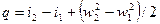
Уравнение (**) показывает, что подведенная теплота в поцессе при течении газа (или жидкости) расходуется на изменение энтальпии и его внешней кинетической энергии.
Когда 1 кг движущегося газа совершает работу lТ (техническую) над внешним объектом и в нем изменяется потенциальная энергия положения (h – h1 –пьезометрическая высота), то закон сохранения энергии приводит к следующему урвнению:
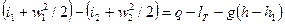 (***)
(***)
или в дифференциальной форме
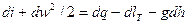 .
.
Полученное уравнение справедливо как для обратимых, так и для необратмых (происходящих с потерями на трение, гидравлических) процессов. Действительно, при наличии трения должна затрачиваться работа трения lтр, которая полностью переходит в теплоту qтр. В силу равенства теплоты на трение и работы на трение, обе величины выпадают из уравнения (***).
Часто рассматривают случай истечения при отсутствии подвода тепла (адиабатный процесс), отсутствия разности потенциальной энергии и технической работы. Уравнение значительно упрощается: di + dw2/2 =0
или i1 –i2 = (w22 – w12)/2 (****)
Изменение внешней кинетической энергии рабочего тела происходит за счет уменьшения его энтальпии. Если начальная скорость потока равна 0 (истечение из ресивера), то скорость течения определяется формулой: 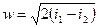 .
.
Скорость истечения и секундный расход идеального газа из суживающегося сопла.
Располагаемая работа при истечении газа с учетом первого закона термодинамики записывается: 
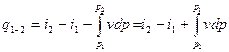
При адиабатном истечении идеального газа
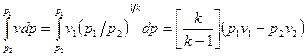 (*****)
(*****)
Скорость истечения
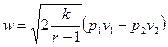 =
=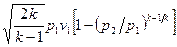 (^)
(^)
При адиабатном истечении идеального газа
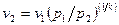
Тогда массовый секундный расход идеального газа
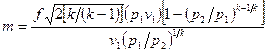
 или
или
m= f√ 2[k/(k-1)](р1/v1)[(р2/р1)2/k – (р2/р1)(k+1)/k] (******)
Массовый секундный расход идеального газа зависит от площади выходного сечения канала, начального состояния газа и степени его расширения.
Анализ уравнения (******) (см. рис) показывает, что при отношении давлений р2/р1, равном единице расход равен 0. С уменьшением давления среды р2 до р2/р1 = βк расход возрастает. При дальнейшем уменьшении давления р2 расход должен падатьи стать равным 0 при отношении р2/р1 равном нулю.Практика подтвердила только совпадение расчетных расходов газа до значений перепада, равного βк. При дальнейшем снижении давления р2 расход не падает.
Для объяснения этого явления Сен-Венан и Вантцель предположили, что для значений βк < р2/р1 < 1 давление в устье суживающего устройства равно давлению среды, куда происходит истечение. Для значений 0< р2/р1< βк давление в узком сечении не меняется вплоть до глубокого вакуума в среде истечения.
Выше отмечалось, что при р2/р1 = βк массовый секундный расход газа достигает максимума. В уравнении (******) переменной частью является [(р2/р1)2/k – (р2/р1)(k+1)/k], поэтому для отыскания максимума следует взять первую производную от этой величины и приравнять 0. Отношение давлений β = р2/р1, обращающее производную в ноль и назовем βк, критическим перепадом давлений.
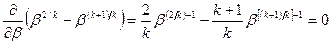
откуда
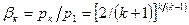
Величина βк зависит только от показателя адиабаты k, т.е. зависит от природы вещества.
Для одноатомного газа k = 1,66 и βк =0,49
Для двухатомного газа k = 1,4 и βк = 0,528
Для трехатомного газа k = 1,3 и βк =0,546
Давление в узком сечении канала, при котором достигается максимальный расход (или критическое даление), определится: рк = βкр1
Величину скорости, которая возникает в узком сечении канала при кртическом перепаде давлений, можно определить с помощью уравнения (^), если вместо отношения давлений р2/р1 подставить значение βк.
После несложных преобразований получим
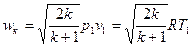 (^^)
(^^)
Величина скорости потока равна скорости звука а:
 |
а = √kRТ
Теперь можно объяснить факт постоянства расхода при перепадах давлений больших критического. Из физики известно, что сигнал об изменении условий в среде передается со скоростью звука. Пока скорость потока меньше скорости звука, то сигнал об изменении статического давления хоть и сносится потоком, но скорость сигнала выше скорости потока и сигнал проходит в обратном направлении. Если же скорость потока равна скорости звука, то находящийся до критического сечения поток не знает об изменении статического давления и не имеет возможности разгоняться. Это явление назвали кризисом течения в сужающемся сопле.
Как же обеспечить увеличение скорости выше скорости звука в канале? Оказалось, что это обеспечивается специальным профилированием канала. При перепадах давлений больше критического площадь сечения канала за горлом должна не уменьшаться, а увеличиваться. Тогда поток заполняет все сечение канала, и скорость потока имеет возможность расти при неизменном расходе газа. Простейшим устройством является сопло Лаваля. При увеличении перепада давлений длина сверхзвуковой части сопла с постепенно увеличивающейся выходной площадью должна возрастать. Сопла ракет первых ступеней более короткие, а сопла последних ступеней ракет, работающих при громадных перепадах давлений (статические давления в космосе мало отличаются от 0), имеют значительную протяженность и размер выходного диаметра.
Интересную особенность воздействий на поток в канале постоянного сечения при желании иметь равномерноускоряющийся поток по длине канала предложил профессор Вулис.
По длине канала сохраняется условие обеспечения прохода массового расхода газа
m = f·w·v
В дозвуковой части канала постоянного сечения для увеличения скорости w можно по длине канала (уменьшение проходного сечения производить нельзя по условию постоянства канала)
- понижать удельный объем (например, подогревая газ).
- можно и добавлять по длине канала расход газа.
После того как в одном из сечений возникнет скорость потока, равная скорости звука, для дальнейшего роста скорости потока потребуется (понимая, что увеличение площади проходного сечения в канале постоянного сечения обеспечить нельзя):
- уменьшая удельный объем газа (охлаждая его);
- отводить расход газа через щели в боковых поверхностях канала.
Можно заметить, что воздействия на поток в дозвуковой части канала и в сверхзвуковой части канала зеркально противоположные. Это явление назвали принципом обращения воздействия.
Следует особо сказать о потерях на трение в канале. Работа сил трения переходит в теплоту. Поэтому, в дозвуковой части канала наличие трения является желательным, а в сверхзвуковой части сопла трение играет обратную роль (тормозит поток).
С термодинамической точки зрения интересно рассмотреть параметры потока и определить предельное значение скорости потока.
Увеличение скорости потока происходит из-за уменьшения энтропии газа.Выше мы получили уравнение i1 –i2 = (w22 – w12)/2 (****)
Можно трансформировать это уравнение: 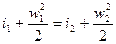
Обозначим левую часть уравнения 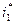 и назовем ее энтальпией торможения. Значение этальпии i будем называть статической энтальпией. Т.е., в потоке рост скорости сопровождается падением энтальпии, названной нами статической. Падает связанная с энтальпией температура (iст = срТст).
и назовем ее энтальпией торможения. Значение этальпии i будем называть статической энтальпией. Т.е., в потоке рост скорости сопровождается падением энтальпии, названной нами статической. Падает связанная с энтальпией температура (iст = срТст).
Если рассматривать адиабатное течения потока, то 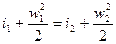 = const
= const
Следовательно, срТст + w2/2 = const. Увеличение скорости приводит к снижению температуры потока. До каких величин может возрасти скорость? Ограничением является значение температуры в потоке. Температура не может опуститься ниже абсолютного нуля!
Величина скорости зависит от энтальпии торможения 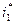 . Большую определенность можно получить, если рассмотреть характеристическую скорость потока, отнеся ее, например, к критической скорости w к по формуле (^^). Относительная величина максимальной скорости зависит от показателя адиабаты и для k= 1,4 это отношение составляет 2,45, а для k= 1,33 отношение равно 2,66. Термодинамика накладывает ограничение на скорость потока.
. Большую определенность можно получить, если рассмотреть характеристическую скорость потока, отнеся ее, например, к критической скорости w к по формуле (^^). Относительная величина максимальной скорости зависит от показателя адиабаты и для k= 1,4 это отношение составляет 2,45, а для k= 1,33 отношение равно 2,66. Термодинамика накладывает ограничение на скорость потока.
Хочется несколько подробнее остановиться на полученном нами понятии параметров торможения потока. При рассмотрении течений в канале оказывается удобным принимать за неизменные параметры энтальпии, давления на входе в канал. В канале происходит переход от полных параметров торможения к статическим. Для энтальпии мы уже получили уравнение связи статической энтальпии срТст и скоростного напора w2/2. Их сумма неизменна по длине канала. Для давлений справедливо следующее равенство:
р* = рст + ρw2/2
В канале без трения неизменным остается сумма статического давления и скоростного напора газа.
V. ЦИКЛЫ РАБОТЫ ТЕПЛОВЫХ МАШИН
5.1 Циклы работы двигателей внутреннего сгорания.
Принцип действия двигателей с подводом тепла при постоянном объеме ясен из рис.5.1, на котором изображена схема и индикаторная диаграмма четырехтактного двигателя.
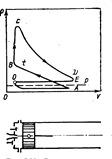
Рис. 5.1. Схема и индикаторная диаграмма поршневого
двигателя внутреннего сгорания
Цикл работы поршневого двигателя с подводом тепла при V = const (Отто) изобразится в координатах p - V (рис.5.2,а) и T – S (рис. 5.2, б):
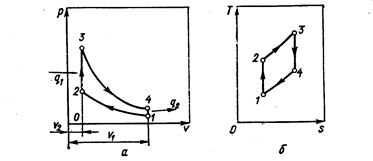
Рис. 5.2. Цикл поршневого двигателя с подводом тепла при V = const.
Здесь 1-2 – адиабатическое сжатие рабочего тела; 2-3 –изохорический подвод тепла; 3 – 4 – адиабатическое расширение рабочего тела; 4 – 1 –условный изохорический процесс отвода тепла, эквивалентный выпуску отработавшего газа. Отношение удельных объемов v1/v2, весьма существенное для характеристики цикла, обозначают в теории поршневых двигателей буквой ε и называют степенью сжатия. Отношение давлений р3 / р2 обозначают буквой λ и называют степенью повышения давления.
Если принять, что рабочее тело – идеальный газ с постоянной теплоемкостью, то термический КПД цикла равен:
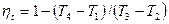 , откуда
, откуда
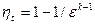 (5.1)
(5.1)
Цикл работы поршневого двигателя с подводом тепла при Р=const (Дизеля) в координатах p – V (рис.32а) и T – S (рис.32, б) изобразится:
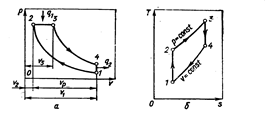
Рис.5.3 Цикл поршневого двигателя с подводом тепла при p = const.
Отношение объемов ν3/ν2 называют степенью предварительного расширения и обозначают в теории поршневых двигателей буквой ρ.
Термический КПД цикла для идеального газа равен:
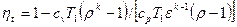 ,
,
или
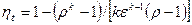 (5.2)
(5.2)
Цикл работы поршневого двигателя со смешанным подводом тепла (цикл Тринклера) приведен на рис. 33
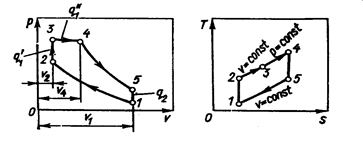
Рис. 5.4. Цикл поршневого двигателя со смешанным подводом тепла.
Теоретический цикл двигателя со смешанным подводом тепла 1-2-3-5-1 состоит из следующих процессов: 1-2 – адиабатическое сжатие рабочего тела; 2-3 – изохорический подвод тепла; 3-4 – изобарический подвод тепла; 4-5 – адиабатическое расширение рабочего тела; 5-1 – изохорический отвод тепла. Термический КПД смешанного цикла
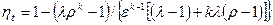 . (5.3)
. (5.3)
5.2. Цикл работы воздушно-реактивных двигателей с подводом тепла при р = const (цикл Брайтона) изобразится в координатах i – S
Рассмотрим первоначально идеальный цикл воздушно-реактивного двигателя (ВРД), т.е. цикл, состоящий из идеальных обратимых процессов. Он состоит из следующих процессов (рис.34):
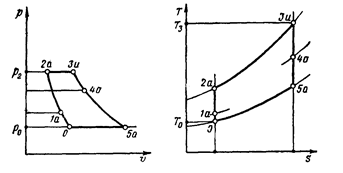
Рис. 5.5. Изображение цикла Брайтона (p = const).
0 – 2а - адиабатическое сжатие, совершаемое в свободной струе перед двигателем за счет скоростного напора (0 -1а) и в компрессоре1а-2а;
2а-3и – изобарический подвод тепла камере сгорания;
3и – 5а – адиабатическое расширение в газовой турбине (3и – 4а) и в реактивном сопле (4а -5а);
5а – 0 – изобарический отвод тепла от струи горячих газов, вытекающих из двигателя во внешнюю среду.
Идеальный цикл ВРД, изображенный на рис. 5.5 контуром 0 – 2а – 3и -5а -0, представляет собой замкнутый цикл работы идеального газа с постоянными химическим составом и теплоемкостью, не зависящей от температуры. Цикл р= const является основным циклом ВРД.
Обозначим символом π = р2 / р0 – степень сжатия рабочего тела.
Термический к.п.д. цикла р = const определяется выражением
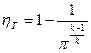 (5.4)
(5.4)
где k = ср/сV = 1,4 – показатель адиабаты для воздуха.
Термический к.п.д. идеального цикла ВРД зависит только от степени сжатия π и с ее увеличением непрерывно растет.
Идеальный и реальный циклы работы условно рассматриваются для одного кг рабочего тела, при этом вместо объема рабочего тела рассматривают удельный объем υ, являющийся обратной величиной плотности рабочего тела.
Площадь, ограниченная контуром 0 – 2а – 3и – 5а – 0, изображает в некотором масштабе полезную работу идеального цикла Lе (ид); эта работа может быть получена в виде приращения кинетической энергии 1 кг воздуха внутри двигателя для создания тяги или в виде механической энергии для привода винтов или энергетической установки.
Напишем уравнение энергии потока для сечений 0 – 0 и 5 – 5:
- Lвн + qI = ср (Т5 – Т0) + (с52 – Vпол2) / 2g (5.5)
где ср (Т5 – Т0) = qII - тепло, отведенное за цикл (изобара 5-0);
Lвн - работа, отобранная от газа и переданная внешнему потребителю.
В общем случае Lвн = Lтурб - Lкомпр ≠ 0
Так как разница между подведенным и отведенным теплом равна полезной работе цикла, т.е. qI - qII = Lе, то уравнение потока (51) сводится к виду
Lе = Lвн + (с52 – Vпол2) / 2g (5.6)
Равенство (5.6) справедливо и для реального цикла ВРД.
Реальный цикл работы при р = const.
Реальный термодинамический цикл существенно отличается от идеального цикла р= const. Он состоит из реальных, т.е. необратимых процессов, сопровождающихся различными потерями и неполнотой сгорания топлива. На рис. 5.6 изображен реальный цикл работы, имеющий с идеальным циклом одинаковые степени сжатия и подогрева рабочего тела.
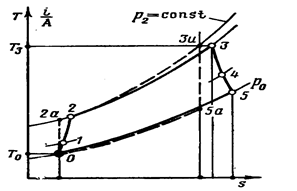
Рис. 5.6. Изображение цикла ВРД при p = const с учетом потерь.
Реальный цикл состоит из:
0 – 1 – 2 – политропическое сжатие с подводом тепла от трения и гидравлических потерь (0 – 1 – процесс динамического сжатия в воздухозаборнике, 2 – 3 –процесс механического сжатия в компрессоре);
2 – 3 – политропический процесс подвода тепла в камере сгорания с наличием потерь давления рабочего тела;
3 – 4 – 5 – процесс политропического расширения (3 – 4 – процесс расширения в турбине; 4 – 5 – расширение в реактивном сопле при наличии потерь на трение как в турбине, так и в сопле);
5 – 0 – изобарический процесс отвода тепла.
Наличие потерь на трение и других гидравлических потерь в процессах сжатия, подвода тепла и при расширении рабочего тела приводит к необходимости уточнения уравнений теплового баланса.
Так, в камере сгорания из-за повышения температуры воздуха за компрессором в реальном цикле по сравнению с идеальным при ограничении максимальной температуры на выходе из камеры сгорания потребное количество топлива уменьшается. Это, вроде бы, плюс с точки зрения термодинамики. При расширении в многоступенчатой турбине из-за наличия потерь в предыдущих ступенях имеет место повышение температуры рабочего тела и повышение работы в последующей ступени. Тоже плюс. Но, в конечном счете, полезная работа в цикле реального двигателя меньше полезной работы идеального цикла работы ВРД.
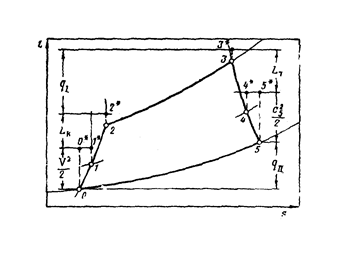
Рис. 5.7. Графическое изображение баланса работ и энергии в цикле p=const.
Изображение действительных состояний рабочего тела в параметрах заторможенного потока в i – S координатах дает возможность в простой и наглядной форме показать изменение полной энергии рабочего тела (для ВРД это воздух и газ) в отдельных элементах ВРД. Здесь введено понятие заторможенных параметров потока. В процессах цикла рабочее тело – газ и воздух, имеют с точки зрения термодинамики параметры потока (так называемые статические значения) и энергию динамического потока газа или воздуха, равного кинетической энергии потока. Суммарные параметры называют параметрами торможения. Они отражают суммарный вклад воздействий на газ в процессе цикла работы. Их условно обозначают верхним значком *. Если этот значок отсутствует, значит речь идет о параметрах внутри потока, так называемых статических. Эти параметры имеют место для любой точки потока внутри его. Именно эти параметры определяют свойства сжимаемости, скорости распространения сигналов внутри потока. Т.е. можно сказать, что с точки зрения физики изучения потока именно статические параметры являются определяющими все явления. Заторможенные параметры представляют собой математическую абстракцию, удобную для составления тепловых балансов.
Рассмотрим изображение цикла ВРД, приведенного на рис.5.7
Можно видеть, что в параметрах торможения для сечений на входе в двигатель и вреактивном сопле имеют место равенства:
i0* = i1* и i4* = i5*
В компрессоре она возрастает в результате подвода механической энергии:
Lк = i2* - i1*,
а в камере сгорания – вследствие подвода тепла:
q1 = i3* - i2*.
В турбине полная энергия газа уменьшается, что обусловлено отводом механической энергии потребителю, компрессору, воздушным винтам, на привод агрегатов топливной и масляной систем двигателя:
Lт = i3* - i4*.
Более полное изучение циклов ПД и ВРД проводится в курсе теории двигателей.
5.2. Циклы паротурбинных установок.
5.2.1. Цикл Карно для водяного пара.
Паротурбинные установки отличаются от двигателей внутреннего сгорания тем, что продукты сгорания топлива являются только промежуточным носителем, а рабочим телом служит пар какой-либо жидкости, чаще всего водяной пар.
В паротурбинных установках процесс получения работы происходит следующим образом (рис. 5.8)
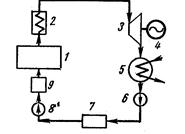
Рис. 5-8.. Схема паротурбинной установки.
Химическая энергия топлива при его сжигании превращается во внутреннюю энергию продуктов сгорания, которая в виде теплоты передается воде и пару в котле 1 и перегревателе 2. Полученный пар направляется в паровуюбину 3, где и происходит преобразование теплоты в механическую работу, а затем обычно в электричекую энерию в электрогенераторе 4. Отработавший пар поступает в конденсатор 5, где отдает отдает теплоту охлаждающей воде. Полученный конденсат конденсационным насосом 6 направляется в питательный бак 7, откуда питательная вода забирается питательным насосом 8, сжимается до давления, равного давлению в котле, и подается через подогреватель 9 в паровой котел.
Как известно, цикл Карно именно так и анализировался автором цикла. Рабочее тело не выбрасывалось в атмосферу. Учитывая, что цикл Карно является самым эффективным из циклов тепловых машин, интересно рассмотреть, как он реализован в паротурбинном водяном цикле.
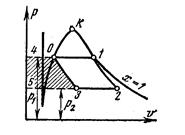
Рис. 5.9. Идеальный цикл Карно
паротурбинной установки
Для насыщенного пара цикл Карно представлен на рис. 5.9. Точка 0 характеризует начальное состояние кипящей воды при давлении р1 . Воде при постоянной температуре Тн1 и постоянном давлении р1 сообщается теплота q1, равная теплоте парообразования r (процесс 0-1). Полученный сухой насыщенный пар о точки 1 расширяется по адиабате в цилинре или турбине до давления р2 (процесс 1-2). В этом процессе температура пара понижается до Тн2 конденсатора и степень сухости понижается от х =1 до х2 . Образовавшийся влажный пар со степенью сухости х2 частично конденсируется при постоянной температуре Тн2 и давлении р2 до точки 3 (процесс 2-3). При этом сухость его уменьшается до х3. От пара отводится теплота q = r2 (х2 – х3). От точки 3 пар по адиабате сжимается в компрессоре до начального состояния, и пар полностью превращается в кипящую воду.
Паротурбинная установка, работающая по циклу Карно, должна состоять из парового котла (процесс 0-1), парового двигателя (поршня или турбины) (процесс 1-2), конденсатора (процесс 2-3) и компрессора (процесс 3-0). Термичесий КПД цикла Карно, где в качестве рабочего тела используют насыщенный пар, определяется по уравнению
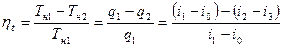
Применение перегретого пара в цикле Карно не увеличивают его КПД, если пределы температур остаются без изменения.
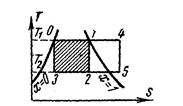
Рис. 5.10. Цикл Карно в TS-диаграмме.
На рис.5.10 цикл Карно для нясыщенного пара изображается площадью 01230, а для перегретого пара – пл. 04530. Из рисунка видно, что КПД обоих циклов одинаковы.
Паросиловые установки, работающие по циклу Карно, имеют существенные недостатки, которые делают нецелесообразным их применение. Эти недостатки заключаются в следующем: в процессе 2-3 конденсация пара осуществляется не полностью, вследствие чего объем цилиндра компрессора при адиабатном сжатии влажного пара от точки 3 до точки0 при давлении р2 должен быть весьма значительным, что увеличивает металлоемкость и габариты машины. Размеры цилиндра компрессора увеличиваются с возрастанием начального давления пара и уменьшением давления в конденсаторе,т.е при переходе к более выгодным темпратурным режимам. Кроме того, необходимость осуществления цикла Карно только в области двухфазных состояний не позволяет иметь высокую начальную температуру пара, ограниченную в пределах пределами критической температуры, что ставит ограничения по дальнейшему повышению термического КПД цикла.
Главное же заключается в том, что затрачиваемая действительная работа на привод компрессора значительно больше теоретической вследствие наличия в нем больших потерь, связанных с необратимостью протекающих процессов. Эти потери могут увеличить действительную работу по сравнению с теоретической на 50% и выше.
Цикл Ренкина.
За основной цикл в паротурбинной устаноке принят цикл Ренкина. В этом цикле осуществляется полная конденсация рабочего тела в конденсаторе, вследствие чего вместо громоздкого малоэффективного компрессора для подачи воды в котел применяют питательный водяной насос, который имеет малый габарит и высокий КПД. Кроме того, в цикле Ренкина возможно применение перегретого пара, что позволяет повыситьсреднеинтегальнуютемпературу подвода теплоты и тем самым увеличить термический КПД цикла.
На рис. 5.11 изображен идеальный цикл Ренкина в pv- диаграмме. Точка 4 характеризует состояние кипящей воды в котле; затем пар подсушивается в в перегревателе – процесс 5-6, 6-1 перегрева пара при давлении р1. Полученный пар по адиабате 1-2 расширяется до давления р2 в конденсаторе. В процессе 2-2/ пар полностью конденсируется до состояния кипящей жидкости при давлении р2, отдавая теплоту парообразования охлаждающей воде.
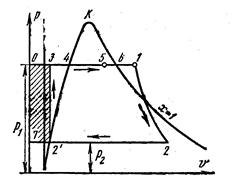
Рис.5.11. Цикл Ренкина для паротурбинной установки
Процесс сжатия воды 2/-3 осуществляется в насосе; полчающееся при этом поышение температуры воды ничтожно мало, и им в иследованиях до давлений 30-40 бар пренебрегают. Линия 3-4 изображает изменение объема воды при нагревании от температуре в конденсаторе до температуры кипения. Работа насоса изображается заштрихованной пл. 032/7.
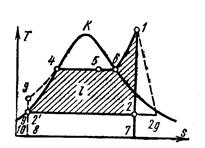
Рис.5.12. Цикл Ренкина в TS – диаграмме.
Энтальпия пара при выходе из перегревателя в точке 1 равна i1 и на TS-диаграмме (рис.5.12) изображается пл. 92/34617109. Энтальпия пара при входе в конденсатор в точке 2 равна i2 и на TS-диаграмме изобажается пл.92/27109. Энтальпия воды при выходе из конденсатора в точке 2/ равна i2/ и на TS-диаграмме изображается пл. 92/8109. Полезная работа пара в цикле Ренкина изображается на pv - диаграмме пл.2/346122/.
Если в цикле Ренкина учитывать работу насоса, то процесс адиабатного сжатия воды в нем представится на TS-диаграмме адиабатой 2/-3, а изобара 3-4 соответствует нагреванию воды в котле при давлении р1 до соответствующей температуры кипения.
 2014-02-12
2014-02-12 848
848








