Сложное движение точки. Теоремы сложения скоростей и ускорений при сложном движении точки

Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁).

Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону).

Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона). Теорема о сложении скоростей: 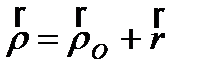, 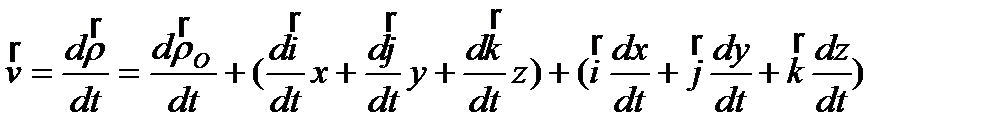; 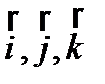-орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца 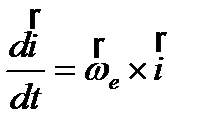и т.д., Þ: ,

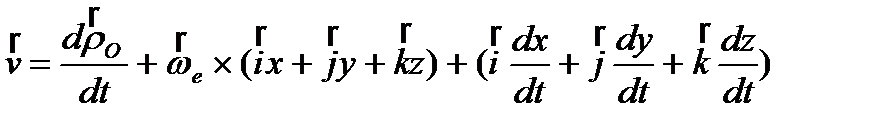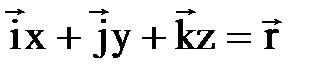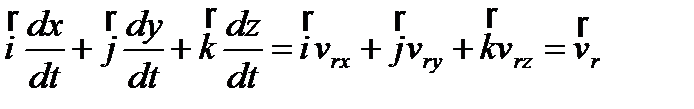; – относительная скорость.

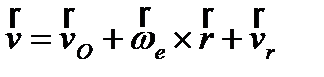; переносная скорость: 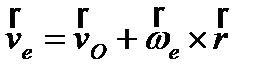, поэтому абсолютная скорость точки = геометрической сумме ее переносной (v_e) и относительной (v_r) скоростей 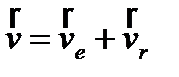, модуль: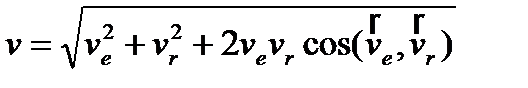

Теорема о сложении ускорений (теорема Кориолиса):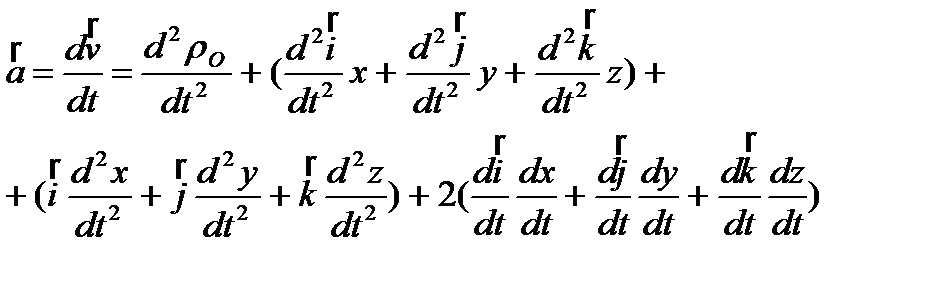

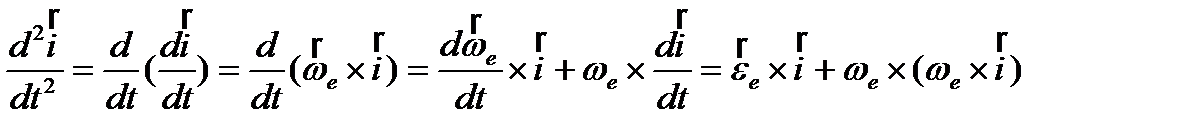и т.д. Слагаемые выражения, определяющего ускорения 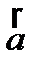: 1) 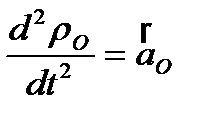– ускорение полюса О;

2)

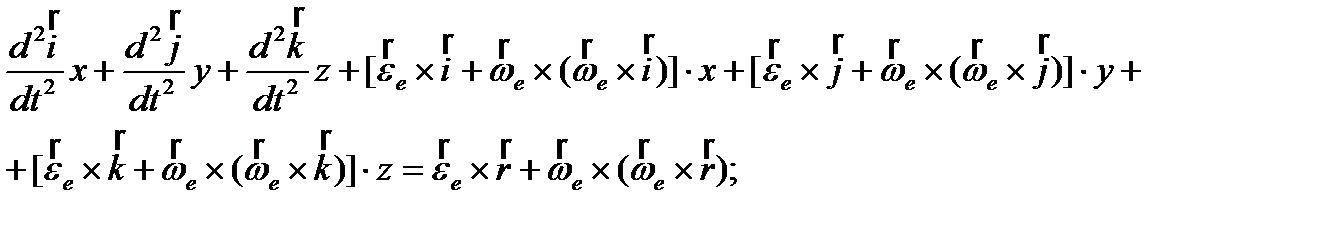
3) 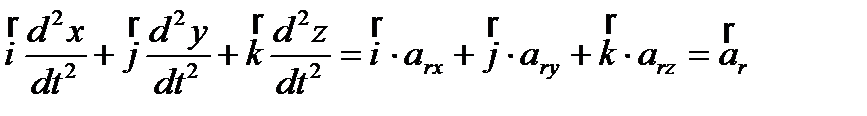– относительное ускорение точки;

4) ,

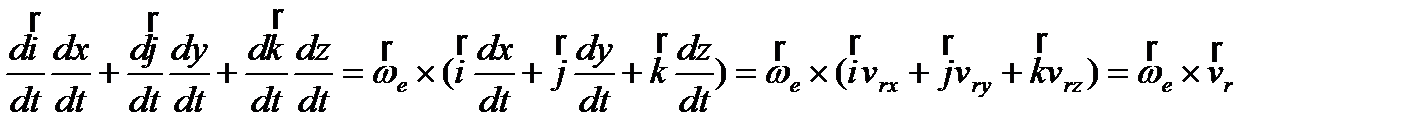получаем: .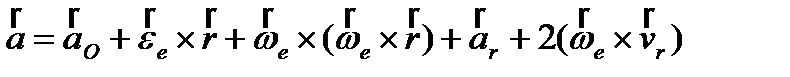

Первые три слагаемых представляют собой ускорение точки в переносном движении: 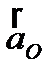– ускорение полюса О; 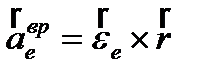– вращательное уск., 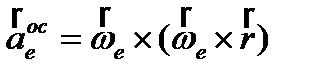– осестремительное уск., т.е. 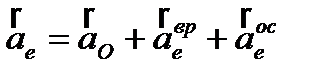. Теорема о сложении ускорений (теорема Кориолиса): 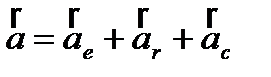, где 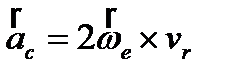– ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует:

1) изменение модуля и направления переносной скорости точки из-за ее относительного движения;

2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: а_с= 2×|w_e×v_r|×sin(w_e^{^}v_r), направление вектора 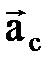определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90^о в направлении вращения.

Кориолисово уск. = 0 в трех случаях:

1) w_e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0;

2) v_r=0; 3) sin(w_e^{^}v_r)=0, т.е. Ð(w_e^{^}v_r)=0, когда относительная скорость v_r параллельна оси переносного вращения. В случае движения в одной плоскости – угол между v_r и вектором w_e = 90^о, sin90^o=1, а_с=2×w_e×v_r.