Имеются две системы отсчета: называемая неподвижной система S, в которой будут написаны все формулы, и подвижная 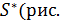 4.12).
4.12).
| Рис. 4.12. Системы отсчета |
| • |
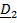 |
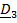 |
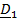 |
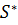 |
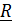 |
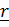 |
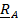 |
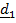 |
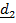 |
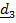 |
| S |
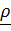 |
Движение точки по отношению к неподвижной системе называется абсолютным; скорость и ускорение обозначаются 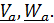
Движение точки по отношению к подвижной системе называется относительным; скорость и ускорение обозначаются 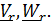
Движение подвижной системы по отношению к неподвижной называется переносным; скорость и ускорение того места подвижной системы, где в данный момент находится рассматриваемая точка, обозначаются 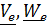 . Вектор положения точки в неподвижной системе может быть представлен в виде суммы
. Вектор положения точки в неподвижной системе может быть представлен в виде суммы 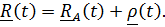 Разложим
Разложим 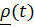 по базису подвижной системы:
по базису подвижной системы:
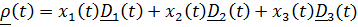 ,
,
где 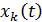 – координаты относительного движения точки. Таким образом,
– координаты относительного движения точки. Таким образом,
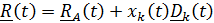 . (4.26)
. (4.26)
Для упрощения записи формул далее символ зависимости величин от времени опустим.
Дифференцируя (4.26) и заменяя по формуле Эйлера 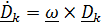 , где
, где 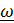 – угловая скорость подвижной системы, получим:
– угловая скорость подвижной системы, получим:
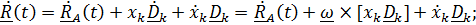
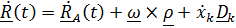 . (4.27)
. (4.27)
Первые два слагаемых – уже знакомая скорость того места подвижной системы, где находится наблюдаемая точка, т. е. переносная скорость
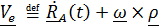 , (4.28)
, (4.28)
а сумма произведений производных относительных координат 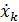 и базисных векторов подвижной системы
и базисных векторов подвижной системы 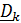 является относительной скоростью:
является относительной скоростью:
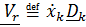 . (4.29
. (4.29
Итак, абсолютная скорость равна сумме переносной и относительной:
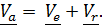 (4.30)
(4.30)
Продифференцируем (4.27): 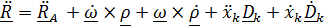 .
.
Подставив в это выражение 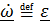 – вектор углового ускорения подвижной системы, ранее полученную формулу (см. 4.27)
– вектор углового ускорения подвижной системы, ранее полученную формулу (см. 4.27) 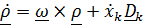 , формулу Эйлера
, формулу Эйлера 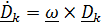 ,получим:
,получим:
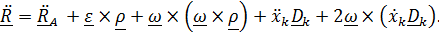
Первые три слагаемые – ускорение того места подвижной системы, где находится точка, т.е. переносное ускорение
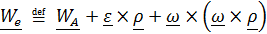 , (4.31)
, (4.31)
сумма произведений производных относительных координат 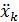 и базисных векторов подвижной системы
и базисных векторов подвижной системы 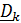 является относительным ускорением
является относительным ускорением
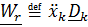 , (4.32)
, (4.32)
а последнее слагаемое называется ускорением Кориолиса
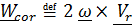 . (4.33)
. (4.33)
Получили теорему о сложении ускорений (теорему Кориолиса):
а бсолютное ускорение равно сумме переносного ускорения, относительного и ускорения Кориолиса:
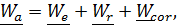 (4.34)
(4.34)
где 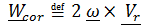 .
.
Заметим, что скорость 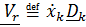 и ускорение
и ускорение 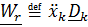 обычно называют относительными скоростью и ускорением, измеряемыми «подвижным наблюдателем», что не совсем верно, поскольку для подвижного наблюдателя подвижный базис
обычно называют относительными скоростью и ускорением, измеряемыми «подвижным наблюдателем», что не совсем верно, поскольку для подвижного наблюдателя подвижный базис 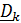 является неподвижным;
является неподвижным; 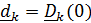 , т. е. «истинные» относительные скорость и ускорение
, т. е. «истинные» относительные скорость и ускорение 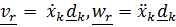 , а
, а 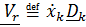 и ускорение
и ускорение 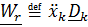 – это повернутые вместе с подвижной системой «истинные».
– это повернутые вместе с подвижной системой «истинные».
Все изложенное можно кратко получить, используя тензор поворота. Вектор положения точки в неподвижной системе представим в виде суммы:
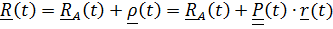 ,
,
где 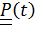 –тензор поворота подвижной системы отсчета;
–тензор поворота подвижной системы отсчета; 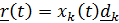 – вектор в неподвижной системе, описывающий относительное движение;
– вектор в неподвижной системе, описывающий относительное движение;
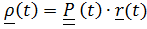 – повернутый вместе с подвижной системой вектор
– повернутый вместе с подвижной системой вектор 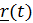 , т.е. вектор относительного положения, каким его видит неподвижный наблюдатель (рис. 4.12). Дифференцируя это равенство и воспользовавшись формулой Пуассона
, т.е. вектор относительного положения, каким его видит неподвижный наблюдатель (рис. 4.12). Дифференцируя это равенство и воспользовавшись формулой Пуассона 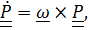 получим теорему сложения скоростей:
получим теорему сложения скоростей:
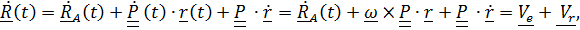
а дифференцируя еще раз – теорему о сложении ускорений:
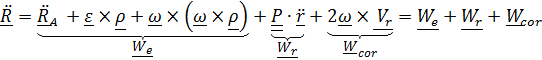 .
.
 2015-02-04
2015-02-04 853
853








