Может случиться, что левая часть дифференциального уравнения
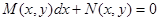 (7)
(7)
является полным дифференциалом некоторой функции 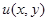 :
:
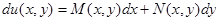 ,
,
и следовательно, уравнение (7) принимает вид 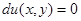 .
.
Если функция 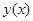 является решением уравнения (7), то
является решением уравнения (7), то  , и, следовательно,
, и, следовательно,
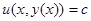 , (8)
, (8)
где  — постоянная, и наоборот, если некоторая функция
— постоянная, и наоборот, если некоторая функция 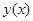 обращает в тождество конечное уравнение (8), то, дифференцируя полученное тождество, получим
обращает в тождество конечное уравнение (8), то, дифференцируя полученное тождество, получим  , и следовательно,
, и следовательно, 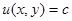 , где
, где  — произвольная постоянная, является общим интегралом исходного уравнения.
— произвольная постоянная, является общим интегралом исходного уравнения.
Если даны начальные значения  , то постоянная
, то постоянная  определяется из (8)
определяется из (8) 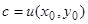 и
и
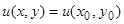 (9)
(9)
является искомым частным интегралом. Если 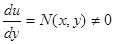 в точке
в точке 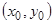 , то уравнение (9) определяет
, то уравнение (9) определяет  как неявную функцию от
как неявную функцию от  .
.
Для того, чтобы левая часть уравнения (7) 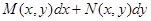 являлась полным дифференциалом некоторой функции
являлась полным дифференциалом некоторой функции 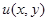 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
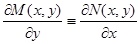 . (10)
. (10)
Если это условие, указанное Эйлером, выполнено, то уравнение (7) легко интегрируется. Действительно, 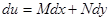 . С другой стороны,
. С другой стороны, 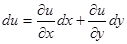 . Следовательно,
. Следовательно,
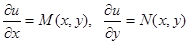 ,
,
откуда 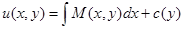 .
.
При вычислении интеграла 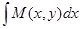 величина
величина  рассматривается как постоянная, поэтому
рассматривается как постоянная, поэтому 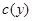 является произвольной функцией от
является произвольной функцией от  . Для определения функции
. Для определения функции 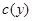 дифференцируем найденную функцию
дифференцируем найденную функцию 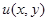 по
по  и, так как
и, так как  , получим
, получим
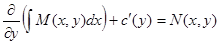 .
.
Из этого уравнения определяем 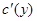 и, интегрируя, находим
и, интегрируя, находим 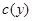 .
.
Как известно из курса математического анализа, еще проще можно определить функцию 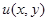 по ее полному дифференциалу
по ее полному дифференциалу 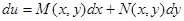 , взяв криволинейный интеграл от
, взяв криволинейный интеграл от 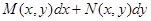 между некоторой фиксированной точкой
между некоторой фиксированной точкой 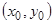 и точкой с переменными координатами
и точкой с переменными координатами  по любому пути:
по любому пути:
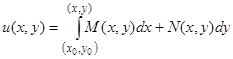 .
.
Чаще всего в качестве пути интегрирования удобно брать ломаную, составленную из двух звеньев, параллельных осям координат; в этом случае
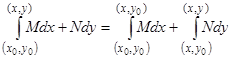
или 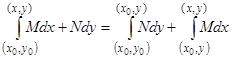 .
.
Пример. 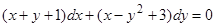 .
.
Левая часть уравнения является полным дифференциалом некоторой функции 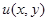 , так как
, так как
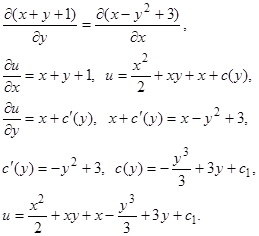
Следовательно, общий интеграл имеет вид
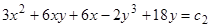 .
.
Можно применить и другой метод определения функции 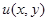 :
:
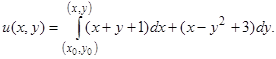
За начальную точку 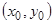 выбираем, например, начало координат, в качестве пути интегрирования —ломаную. Тогда
выбираем, например, начало координат, в качестве пути интегрирования —ломаную. Тогда
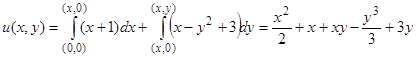
и общий интеграл имеет вид
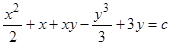 , что совпадает с предыдущим результатом, приводя к общему знаменателю.
, что совпадает с предыдущим результатом, приводя к общему знаменателю.
В некоторых случаях, когда левая часть уравнения (7) не является полным дифференциалом, легко удается подобрать функцию 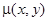 , после умножения на которую левая часть уравнения (7) превращается в полный дифференциал
, после умножения на которую левая часть уравнения (7) превращается в полный дифференциал 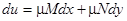 . Такая функция
. Такая функция 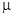 называется интегрирующим множителем. Заметим, что умножение на интегрирующий множитель
называется интегрирующим множителем. Заметим, что умножение на интегрирующий множитель 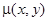 может привести к появлению лишних частных решений, обращающих этот множитель в нуль.
может привести к появлению лишних частных решений, обращающих этот множитель в нуль.
Пример. 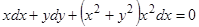 .
.
Очевидно, что после умножения на множитель 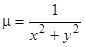 левая часть превращается в полный дифференциал. Действительно, после умножения на
левая часть превращается в полный дифференциал. Действительно, после умножения на 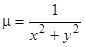 получим
получим
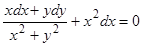
или, интегрируя,  . Умножая на 2 и потенцируя, будем иметь
. Умножая на 2 и потенцируя, будем иметь 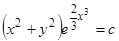 .
.
Конечно, далеко не всегда интегрирующий множитель подбирается столь легко. В общем случае для нахождения интегрирующего множителя надо подобрать хотя бы одно не равное тождественно нулю частное решение уравнения в частных производных 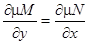 , или в развернутом виде
, или в развернутом виде
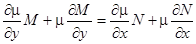 ,
,
которое после деления на 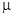 и переноса некоторых слагаемых в другую часть равенства приводится к виду
и переноса некоторых слагаемых в другую часть равенства приводится к виду
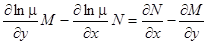 . (11)
. (11)
В общем случае интегрирование этого уравнения в частных производных является задачей отнюдь не более простой, чем интегрирование исходного уравнения, однако в некоторых случаях подбор частного решения уравнения (11) не представляет затруднений.
Кроме того, считая, что интегрирующий множитель является функцией только одного аргумента (например, является функцией только 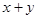 или только
или только 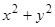 , или функцией только
, или функцией только  , или только
, или только  и т.д.), можно уже без труда проинтегрировать уравнение (11) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель легко может быть найден.
и т.д.), можно уже без труда проинтегрировать уравнение (11) и указать условия, при которых интегрирующий множитель рассматриваемого вида существует. Тем самым выделяются классы уравнений, для которых интегрирующий множитель легко может быть найден.
Например, найдем условия, при которых уравнение  имеет интегрирующий множитель, зависящий только от
имеет интегрирующий множитель, зависящий только от  , т.е.
, т.е. 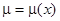 . При этом уравнение (11) упрощается и приобретает вид
. При этом уравнение (11) упрощается и приобретает вид 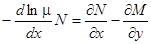 , откуда, считая
, откуда, считая 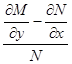 непрерывной функцией от
непрерывной функцией от  , получим
, получим
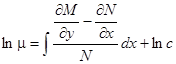 ,
,
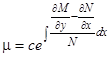 . (12)
. (12)
Можно считать 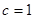 , так как достаточно иметь лишь один интегрирующий множитель.
, так как достаточно иметь лишь один интегрирующий множитель.
Если 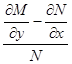 является функцией только от
является функцией только от  , то интегрирующий множитель, зависящий лишь от
, то интегрирующий множитель, зависящий лишь от  , существует и равен (12), в противном случае интегрирующего множителя вида
, существует и равен (12), в противном случае интегрирующего множителя вида 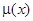 не существует.
не существует.
Условие существования интегрирующего множителя, зависящего только от  , выполнено, например, для линейного уравнения
, выполнено, например, для линейного уравнения  или
или 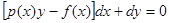 . Действительно,
. Действительно, 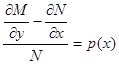 и, следовательно,
и, следовательно, 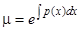 . Совершенно аналогично могут быть найдены условия существования интегрирующих множителей вида
. Совершенно аналогично могут быть найдены условия существования интегрирующих множителей вида 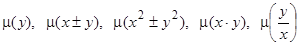 и т.д.
и т.д.
Пример. Имеет ли уравнение 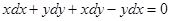 интегрирующий множитель вида
интегрирующий множитель вида 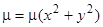 ?
?
Обозначим 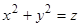 . Уравнение (11) при
. Уравнение (11) при 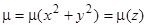 принимает вид
принимает вид 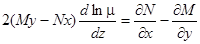 , откуда
, откуда 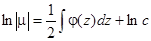 или
или
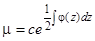 (13)
(13)
где 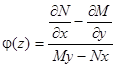 .
.
Для существования интегрирующего множителя заданного вида необходимо и в предположении непрерывности 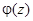 достаточно, чтобы
достаточно, чтобы 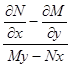 была функцией только
была функцией только 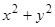 . В данном случае
. В данном случае 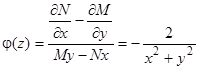 , следовательно, интегрирующий множитель
, следовательно, интегрирующий множитель 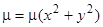 существует и равен (13). При
существует и равен (13). При 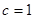 получим
получим 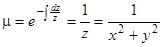 . Умножая исходное уравнение на
. Умножая исходное уравнение на 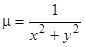 , приведем его к виду
, приведем его к виду

или 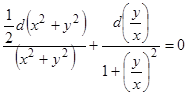 ,
, 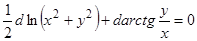 .
.
Интегрируя, получим 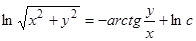 , а после потенцирования будем иметь
, а после потенцирования будем иметь 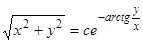 , или в полярных координатах
, или в полярных координатах 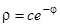 — семейство логарифмических спиралей.
— семейство логарифмических спиралей.
Пример. Найти форму зеркала, отражающего параллельно данному направлению все лучи, выходящие из заданной точки.
Поместим начало координат в заданную точку и направим ось абсцисс параллельно заданному в условиях задачи направлению. Пусть луч падает на зеркало в точке 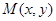 . Рассмотрим сечение зеркала плоскостью
. Рассмотрим сечение зеркала плоскостью 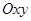 , проходящее через ось абсцисс и точку
, проходящее через ось абсцисс и точку 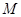 . Проведем касательную
. Проведем касательную 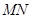 к рассматриваемому сечению поверхности зеркала в точке
к рассматриваемому сечению поверхности зеркала в точке 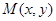 . Так как угол падения луча равен углу отражения, то треугольник
. Так как угол падения луча равен углу отражения, то треугольник 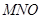 — равнобедренный. Следовательно,
— равнобедренный. Следовательно,
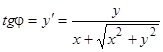 .
.
Полученное однородное уравнение легко интегрируется заменой переменных 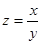 , но еще проще, освободившись от иррациональности в знаменателе, переписать его в виде
, но еще проще, освободившись от иррациональности в знаменателе, переписать его в виде 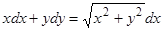 . Это уравнение имеет очевидный интегрирующий множитель
. Это уравнение имеет очевидный интегрирующий множитель 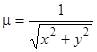 ,
, 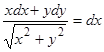 ,
, 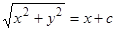 ,
, 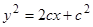 (семейство парабол).
(семейство парабол).
Эта задача еще проще решается в координатах  и
и 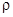 , где
, где  , при этом уравнение сечения искомых поверхностей приобретает вид
, при этом уравнение сечения искомых поверхностей приобретает вид  .
.
Можно доказать существование интегрирующего множителя, или, что то же самое, существование ненулевого решения уравнения в частных производных (11) в некоторой области, если функции 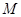 и
и 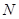 имеют непрерывные производные и по крайней мере одна из этих функций не обращается в нуль. Следовательно, метод интегрирующего множителя можно рассматривать как общий метод интегрирования уравнений вида
имеют непрерывные производные и по крайней мере одна из этих функций не обращается в нуль. Следовательно, метод интегрирующего множителя можно рассматривать как общий метод интегрирования уравнений вида  , однако ввиду трудности нахождения интегрирующего множителя этот метод чаще всего применяется в тех случаях, когда интегрирующий множитель очевиден.
, однако ввиду трудности нахождения интегрирующего множителя этот метод чаще всего применяется в тех случаях, когда интегрирующий множитель очевиден.
 2014-02-02
2014-02-02 3543
3543
