Лекция 1. При изучении физических явлений часто не удается непосредственно найти законы, связывающие величины

При изучении физических явлений часто не удается непосредственно найти законы, связывающие величины, характеризующие физическое явление, но в то же время легко устанавливается зависимость между теми же величинами и их производными или дифференциалами. При этом мы получаем уравнения, содержащие неизвестные функции или вектор-функции под знаком производной или дифференциала.

Уравнения, в которых неизвестная функция или вектор-функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями. Приведем несколько примеров дифференциальных уравнений: (либо, можно сказать, рассмотрим ряд типичных задач физики и механики, изучение которых методом математического моделирования приводит к исследованию дифференциальных уравнений):

1) 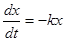— уравнение радиоактивного распада (— постоянная распада, — количество неразложившегося вещества в момент времени 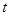, скорость распада 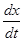пропорциональна количеству распадающегося вещества).

2) 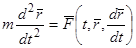— уравнение движения точки массы 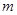под влиянием силы 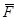, зависящей от времени, положения точки, определяемого радиус-вектором , и ее скорости 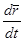. Сила равна произведению массы на ускорение.

3) 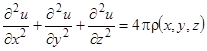— уравнение Пуассона, которому, например, удовлетворяет потенциал 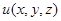электростатического поля, 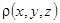— плотность зарядов.

Зависимость между искомыми величинами будет найдена, если будут указаны методы нахождения неизвестных функций, определяемых дифференциальными уравнениями. Нахождение неизвестных функций, определяемых дифференциальными уравнениями, и является основной задачей теории дифференциальных уравнений.

Если в дифференциальном уравнении неизвестные функции или вектор-функции являются функциями одной переменной, то дифференциальное уравнение называется обыкновенным (например, первые два уравнения из примеров). Если же неизвестная функция, входящая в дифференциальное уравнение, является функцией двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных (например, третье уравнение).

Порядком дифференциального уравнения называется максимальный порядок входящей в уравнение производной (или дифференциала) неизвестной функции.

Решением дифференциального уравнения называется функция, которая при подстановке в дифференциальное уравнение обращает его в тождество.

Например,уравнение радиоактивного распада

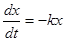(1)

имеет решени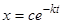е , где — произвольная постоянная.

Очевидно, что дифференциальное уравнение (1) еще не полностью определяет закон распада 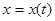. Для его полного определения надо знать количество распадающегося вещества 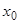в некоторый начальный момент времени . Если 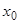известно, то, принимая во внимание условие 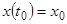, из решения уравнения (1) находим закон радиоактивного распада: .

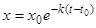Одной из важных характеристик процесса радиоактивного распада является период полураспада — промежуток времени 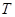, за который количество распадающегося вещества уменьшается вдвое. Из решения найдем 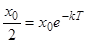, откуда .

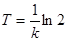Отметим, что рассмотренное уравнение является математической моделью не только процесса радиоактивного распада, но и многих других процессов деления или размножения, характеризуемых тем, что скорость деления (размножения) пропорциональна количеству вещества в данный момент времени, причем коэффициент пропорциональности есть некоторая постоянная, характеризующая рассматриваемый процесс.

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. В рассмотренном примере мы легко нашли точное решение, однако в более сложных случаях очень часто приходится применять приближенные методы интегрирования дифференциальных уравнений. Эти приближенные методы еще недавно приводили к утомительным вычислениям, но теперь есть компьютеры.

Рассмотрим несколько подробнее упомянутую выше более сложную задачу о нахождении закона движения 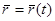материальной точки массы 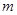под действием заданной силы 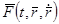. По закону Ньютона

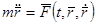. (2)

Следовательно, задача сводится к интегрированию этого дифференциального уравнения. Очевидно, что закон движения еще не вполне определяется заданием массы 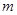и силы 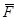, надо еще знать начальное положение точки

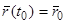(2.1)

и начальную скорость

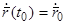. (2.2)

Рассмотрим весьма естественный приближенный метод решения уравнения (2) с начальными условиями (2.1) и (2.2), причем идея этого метода может служить и для доказательства существования решения рассматриваемой задачи.

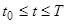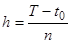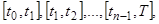Разделим отрезок времени , на котором требуется определить решение уравнения (2), удовлетворяющее начальным условиям (2.1) и (2.2), на равных частей длины : где .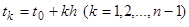

В пределах каждого из этих малых (при больших значениях ) отрезков времени сила 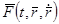мало изменяется (вектор-функция 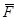предполагается непрерывной), поэтому приближенно ее можно считать на каждом отрезке 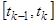постоянной, например, равной ее значению в левой граничной точке каждого отрезка. Точнее, на отрезке 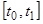сила 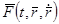считается постоянной и равной . При этом допущении из уравнения (2) и начальных условий (2.1) и (2.2) легко определяется закон движения 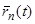на отрезке 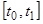(движение будет равномерно переменным) и, следовательно, в частности, известны значения 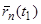и 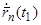. Тем же методом приближенно определяем закон движения 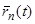на отрезке 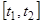, считая силу 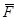на этом участке постоянной и равной 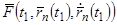. Продолжая этот процесс, определим приближенное решение 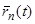поставленной задачи с начальными значениями для уравнения (2) на всем отрезке .

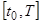Интуитивно ясно, что при 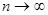приближенное решение 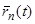должно стремиться к точному решению.

Заметим, что векторное уравнение (2) второго порядка может быть заменено эквивалентной системой двух векторных уравнений первого порядка, если рассматривать скорость 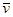как вторую неизвестную вектор-функцию:

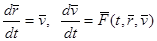. (3)

Каждое векторное уравнение в трехмерном пространстве может быть заменено путем проектирования на оси координат тремя скалярными уравнениями. Следовательно, уравнение (2) эквивалентно системе трех скалярных уравнений второго порядка, а система (3) эквивалентна системе шести скалярных уравнений первого порядка.

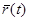Наконец, можно одно векторное уравнение (2) второго порядка в трехмерном пространстве заменить одним векторным уравнением первого порядка в шестимерном пространстве, координатами в котором служат координаты радиуса-вектора и координаты 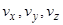вектора скорости 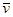. Такое пространство называется фазовым. Радиус-вектор 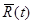в таком пространстве имеет координаты 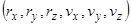. В таких обозначениях система (3) имеет вид

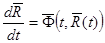(4)

(проекциями вектора 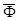в шестимерном пространстве служат соответствующие проекции правых частей системы (3) в трехмерном пространстве).

При такой интерпретации начальные условия (2.1) и (2.2) заменяются условием

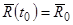. (4.1)

Решением уравнения (4) 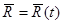будет фазовая траектория, каждой точке которой будем соответствовать некоторое мгновенное состояние движущейся точки — ее положение 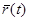и ее скорость .

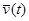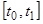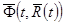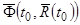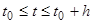
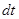Если к уравнению (4) с начальным условием (4.1) применить приближенный метод, который мы рассмотрели ранее, то на первом отрезке вектор-функцию надо считать постоянной и равной . Итак, при , откуда, умножая на и интегрируя в пределах от до 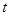, получим линейную вектор-функцию :

.

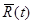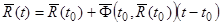В частности, при будем иметь . Повторяя то же рассуждение на следующих участках, получим

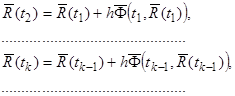
Применяя эти формулы раз, дойдем до значения .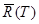

В этом методе искомое решение 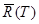приближенно заменяется кусочно-линейной вектор-функцией, графиком которой служит некоторая ломаная, называемая ломаной Эйлера.

Для уравнения (2) нередко в приложениях встречается и иная постановка задачи — дополнительные условия задаются не в одной, а в двух точках. Такая задача, в отличие от задачи с условиями (2.1) и (2.2), называемой задачей с начальными условиями или задачей Коши, носит название краевой или граничной.

Важным частным случаем уравнения (2) является уравнение колебаний физического маятника. Обычно физическим маятников называют абсолютно твердое тело, которое может вращаться под действием силы тяжести вокруг неподвижной оси, не проходящей через центр тяжести С.

Рассмотри сечение данного тела плоскостью, перпендикулярной оси вращения и проходящей через центр тяжести. Точку пересечения оси вращения с данной плоскостью обозначим О. Очевидно, положение физического маятника в любой момент времени можно характеризовать углом , который составляет прямая ОС с вертикальной осью 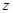, проходящей через точку О. Для вывода уравнения движения воспользуемся вторым законом Ньютона в применении к вращательному движению (угловое ускорение пропорционально главному моменту внешних сил). Тогда, пренебрегая силами сопротивления, получим

, (5)

где 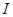— момент инерции тела относительно оси вращения, а — расстояние от точки О до центра тяжести С.

Общее уравнение (5) колебаний физического маятника является нелинейным. В случае малых колебаний, ограничиваясь первым слагаемым разложения функции 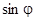в ряд, получим

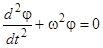, (6)

где 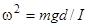. Очевидно, размерность 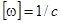, что и оправдывает введенное обозначение. Заметим, что в случае уравнения (6) возвращающая сила пропорциональна смещению от положения равновесия.

Непосредственной проверкой можно убедиться, что уравнение (6) имеет периодические решения частоты : 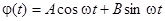, где А и В — произвольные постоянные, определяющие амплитуду периодических колебаний.

Если же мы учтем силы сопротивления, которые пропорциональны угловой скорости, то уравнение (6) перейдет в уравнение вида 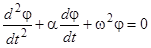. Такое уравнение определяет затухающие колебания.

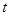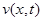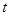Уравнения переноса. Пусть по трубе постоянного поперечного сечения, ось которой совпадает с осью , движется поток воздуха, скорость которого вдоль оси трубы в точке в момент времени есть заданная функция . Пусть воздух переносит некоторое вещество, линейную плотность которого в сечении трубы с координатой в момент времени обозначим 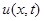. В процессе переноса вещество осаждается на стенках трубы. Будем считать, что плотность распределения осаждающегося вещества задается выражением 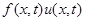(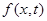— заданная функция), т.е. пропорциональна концентрации вещества. Это значит, что количество вещества, которое осаждается на участке стенки трубы между сечениями и 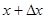за промежуток времени задается законом .

Для получения дифференциального уравнения относительно 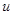рассмотрим баланс вещества в области между сечениями и 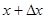. Процесс диффузии не будем учитывать, что естественно, если скорость 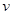достаточно велика.

За время 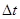изменение количества вещества в рассматриваемой области равно 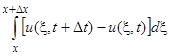. Это изменение определяется, во-первых, разностью потоков вещества: втекающего через сечение и равного 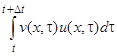и вытекающего через сечение 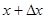и равного , а во-вторых, убылью количества вещества (за счет осаждения на стенке), равной . Таким образом, закон сохранения вещества дает

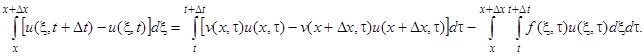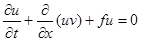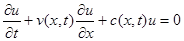Пользуясь теоремой о конечном приращении для подынтегральных выражений в предположении наличия непрерывных частных производных у рассматриваемых функций, вычисляя интегралы по теореме о среднем и преобразуя результат, в силу непрерывности всех слагаемых получим окончательное уравнение , или , где 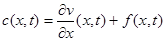. Полученное уравнение является уравнением в частных производных первого порядка. Для него можно поставить, например, следующую задачу. 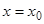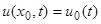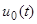Пусть известна концентрация вещества при : , где — заданная функция. Требуется определить 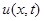для .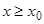

Задача о просачивании воды сквозь песок. Пусть вода просачивается через песок сверху вниз. Направим ось вниз. Через 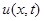обозначим плотность воды в песке. Скорость движения воды 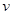, очевидно, зависит от ее плотности, т.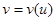е. , где 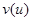есть заданная функция, причем 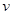возрастает вместе с .

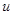Рассмотрим баланс воды в слое 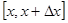. За время 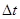изменение количества воды равно 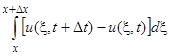. Это изменение происходит за счет разности входящего потока 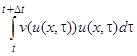и выходящего потока 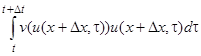. Таким образом,

.

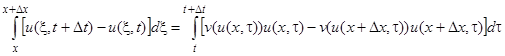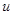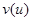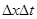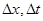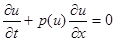Предполагая наличие непрерывных частных производных у и дифференцируемость , применим теорему о конечном приращении и формулу среднего значения для вычисления интегралов. Поделив затем на и устремив к нулю, получим уравнение , или , где 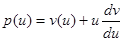— заданная функция от .

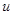Полученное уравнение также является уравнением в частных производных первого порядка. Типичными задачами для него являются: задание функции 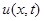при фиксированном значении 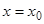— 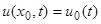(т.е. задана плотность воды на границе слоя песка во все моменты времени) и задание функции 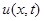для фиксированного момента времени 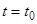— 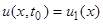(т.е. задано распределение плотности воды по разрезу слоя песка в определенный момент времени ).

Это уравнение сложнее предыдущего. Множитель 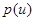в нем зависит от неизвестной функции, в то время как в предыдущем уравнении производные неизвестной функции и сама она входят линейно. Такое уравнение называется квазилинейным.

Колебания упругого стержня. Рассмотрим задачу о малых продольных колебаниях упругого стержня. Пусть в недеформированном состоянии стержень имеет длину 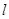, ось его совпадает с осью и в процессе его колебаний под действием внешних сил, направленных по оси , поперечные сечения стержня смещаются как целое, не деформируясь в своей плоскости. Тогда процесс колебаний стержня можно характеризовать одной скалярной функцией 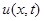— смещением в момент времени 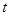сечения стержня, имевшего в недеформированном состоянии координату . Будем рассматривать стержень переменной плотности , подчиняющийся закону Гука: упругая сила, деформирующая бесконечно малый элемент стержня, заключенный между сечениями и 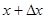, пропорциональна относительному удлинению этого элемента. Коэффициент пропорциональности (модуль упругости) также будем считать переменным вдоль стержня и обозначим его через 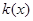. Подсчитаем относительное удлинение 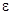выделенного элемента. Очевидно, длина этого элемента в момент времени 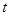равна

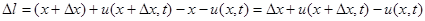, откуда относительное удлинение . Переходя в этом выражении к пределу при 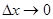, предполагая функцию 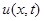непрерывно дифференцируемой и воспользовавшись законом Гука, получим, что сила упругого напряжения в сечении , действующая со стороны правой части на левую, равна 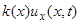. Заметим, что полученное выражение для силы упругого напряжения справедливо лишь в случае малых колебаний, когда можно применять закон Гука к бесконечно малому элементу стержня.

Чтобы получить уравнение колебаний стержня, применим второй закон Ньютона к выделенному элементу. Будем считать, что внешние силы, приложенные к стержню, распределены с плотностью 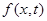, так что импульс силы, действующей на элемент 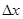за промежуток времени 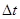, равен 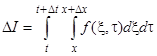. Кроме того, на граничные сечения выделенного элемента действуют определенные выше силы упругого напряжения. Тогда второй закон Ньютона запишется в виде

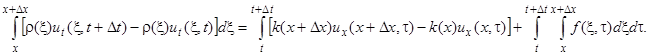Это — интегродифференциальное уравнение колебаний упругого стержня. Предполагая непрерывную дифференцируемость функций, стоящих в квадратных скобках, и непрерывность 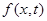, используя теорему о конечных приращениях, вычисляя интегралы по теореме о среднем, преобразуя результат и переходя к пределу при 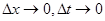, получим окончательно дифференциальное уравнение продольных колебаний упругого стержня

.

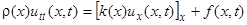Это — уравнение в частных производных второго порядка, являющееся математической моделью колебаний в пространстве и во времени непрерывной упругой среды. В статическом случае (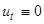) стержень под действием постоянной во времени внешней силы и сил упругого взаимодействия принимает некоторое состояние статического равновесия, которое описывается обыкновенным дифференциальным уравнением

.

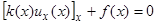Типичной задачей для этого уравнения является краевая задача, когда задаются смещения граничных точек стержня 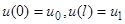, или напряжения, приложенные к граничным сечениям .

Общее уравнение колебаний переходит в обыкновенное дифференциальное уравнение и в тех случаях, когда рассматриваются периодические колебания, происходящие под действием периодической внешней силы. Пусть 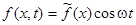. Будем искать решение общего уравнения колебаний также в виде 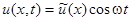. Тогда для 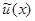— амплитуды периодических колебаний, установившихся в системе под действием периодической внешней силы, получим обыкновенное дифференциальное уравнение . Типичной краевой задачей определения частного решения этого уравнения опять является краевая задача с рассмотренными граничными условиями.

В ряде случаев интерес представляет определение частот собственных колебаний системы — частот тех установившихся периодических колебаний, которые возможны в системе при отсутствии внешних сил, как распределенных, так и сосредоточенных в граничных сечениях. Эта задача сводится к краевой задаче для однородного уравнения. Требуется определить те значения параметра 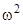, при которых это уравнение имеет нетривиальное решение, удовлетворяющее заданным однородным граничным условиям, например 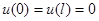. Такая задача носит название краевой задачи о собственных значениях.

Пусть, например, требуется, чтобы материальная точка массы 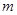, движущаяся под действием силы 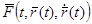, находившаяся в начальный момент 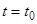в положении 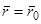, попала бы в момент в положение 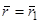, т.е. надо решить уравнение (2) с граничными условиями 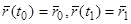. К этой граничной задаче сводятся многие баллистические задачи, причем очевидно, что решение здесь часто может быть не единственным, так как из точки 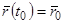можно попасть в точку 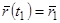по настильной и по навесной траекториям.

Точное или приближенное решение задач с начальными условиями и граничных задач является основной задачей теории дифференциальных уравнений, однако иногда требуется выяснить или приходится ограничиваться выяснением лишь некоторых свойств решений. Например, часто требуется установить, существуют ли периодические или колеблющиеся решения, оценить быстроту возрастания или убывания решений, выяснить, сильно ли меняется решение при малом изменении начальных значений.

Остановимся несколько подробнее на последнем из этих вопросов применительно к уравнению движения (2). В прикладных задачах начальные значения 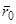и 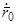почти всегда являются результатом измерения и, следовательно, неизбежно определены с некоторой погрешностью. Поэтому естественно возникает вопрос о влиянии малого изменения начальных значений на искомое решение.

Если сколь угодно малые изменения начальных значений способны вызвать значительные изменения решения, то решение, определяемое неточными начальными значениям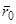и и 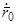, обычно не имеет никакого прикладного значения, так как оно даже приближенно не описывает движение рассматриваемого тела. Следовательно, возникает важный для приложений вопрос о нахождении условий, при которых малое изменение начальных значени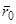й и 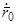вызывает лишь малое изменение определяемого ими решения .

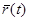Аналогичный вопрос возникает и в задачах, в которых требуется выяснить, с какой точностью надо задавать начальные значения 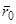и 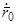, чтобы движущаяся точка с заданной точностью вышла на требуемую траекторию или попала бы в данную область.

Столь же большое значение имеет вопрос о влиянии на решение малых слагаемых в правой части уравнения (2) — малых, но постоянно действующих сил.

В некоторых случаях эти малые силы, действующие в течение большого промежутка времени, способны сильно исказить решение и ими нельзя пренебречь. В других случаях изменение решения под действием этих сил незначительно, и если оно не превосходит требуемой точности вычисления, то малыми возмущающими силами можно пренебречь.

В дальнейшем мы будем рассматривать методы интегрирования дифференциальных уравнений и простейшие способы исследования их решений.