Для производных порядка  введем обозначение
введем обозначение 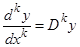 . Пользуясь этим обозначением, запишем уравнение
. Пользуясь этим обозначением, запишем уравнение 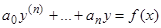 в виде
в виде 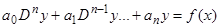 , или
, или
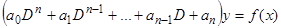 . (9)
. (9)
Выражение 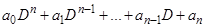 называется операторным полиномом. Этот операторный полином кратко обозначим
называется операторным полиномом. Этот операторный полином кратко обозначим 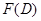 , а уравнение (9) запишем в виде
, а уравнение (9) запишем в виде 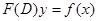 .
.
Непосредственной проверкой легко устанавливается справедливость следующих тождеств:
1) 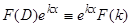 .
.
2) 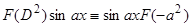 .
.
3) 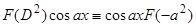 .
.
4) 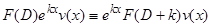 .
.
Действительно:
1) 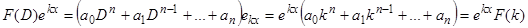 .
.
2) 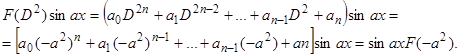
Тождество 3) доказывается аналогично.
4) 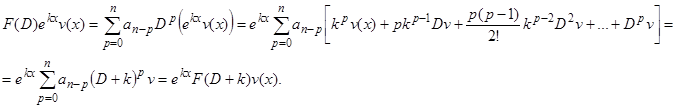
Суммой двух операторов  и
и  называется оператор
называется оператор 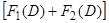 , действие которого на некоторую функцию
, действие которого на некоторую функцию 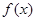 определяется равенством
определяется равенством 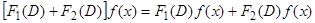 . Из этого определения следует, что
. Из этого определения следует, что 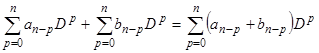 , так как действие левой и правой частей этого равенства на некоторую
, так как действие левой и правой частей этого равенства на некоторую  раз дифференцируемую функцию
раз дифференцируемую функцию 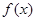 приводит к одному и тому же результату, т.е. правило сложения операторных полиномов не отличается от правила сложения обычных (не операторных) полиномов.
приводит к одному и тому же результату, т.е. правило сложения операторных полиномов не отличается от правила сложения обычных (не операторных) полиномов.
Произведением двух операторов 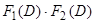 называется оператор, действие которого на некоторую достаточное число раз дифференцируемую функцию
называется оператор, действие которого на некоторую достаточное число раз дифференцируемую функцию 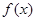 определяется равенством
определяется равенством  , т.е. на функцию
, т.е. на функцию 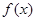 действует сначала правый множитель, а затем на результат действия правого множителя на функцию
действует сначала правый множитель, а затем на результат действия правого множителя на функцию 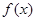 действует левый множитель.
действует левый множитель.
Исходя из этого определения, нетрудно обнаружить, что правило умножения операторных полиномов не отличается от правила умножения обычных (не операторных) полиномов. Действительно,
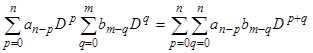 , (10)
, (10)
так как  , что совпадает с результатом действия оператора
, что совпадает с результатом действия оператора 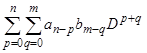 на
на 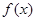 .
.
Из (10), в частности, следует коммутативность умножения операторов 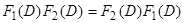 .
.
Справедливость дистрибутивного закона 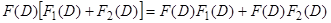 непосредственно следует из правила дифференцирования суммы. Следовательно, действия сложения и умножения с операторными полиномами не отличаются от тех же действий с обычными (не операторными) полиномами.
непосредственно следует из правила дифференцирования суммы. Следовательно, действия сложения и умножения с операторными полиномами не отличаются от тех же действий с обычными (не операторными) полиномами.
Определим теперь оператор 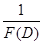 .
.
Результатом действия оператора 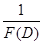 на некоторую непрерывную функцию
на некоторую непрерывную функцию 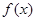 является решение уравнения
является решение уравнения
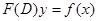 , (11)
, (11)
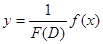 .
.
Следовательно,
 . (12)
. (12)
Можно было бы считать, что 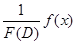 является решением уравнения (11), определяемым какими-нибудь конкретными, например нулевыми, начальными условиями, однако для наших целей удобнее считать, что
является решением уравнения (11), определяемым какими-нибудь конкретными, например нулевыми, начальными условиями, однако для наших целей удобнее считать, что 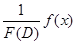 является одним из решений (все равно каким) уравнения (11) и, следовательно, действие оператора
является одним из решений (все равно каким) уравнения (11) и, следовательно, действие оператора 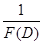 на некоторую функцию
на некоторую функцию 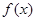 определено лишь с точностью до слагаемого, равного решению соответствующего однородного уравнения.
определено лишь с точностью до слагаемого, равного решению соответствующего однородного уравнения.
При таком понимании действия оператора 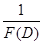 будет справедливым равенство
будет справедливым равенство
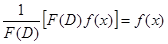 , (13)
, (13)
так как 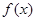 , очевидно, является решением уравнения
, очевидно, является решением уравнения 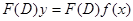 .
.
Произведение операторов 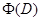 на
на 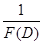 определяется равенством
определяется равенством 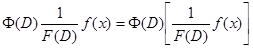 . Аналогично
. Аналогично 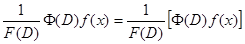 . Поэтому в формулах (12) и (13) скобки можно опустить. Заметим еще, что
. Поэтому в формулах (12) и (13) скобки можно опустить. Заметим еще, что 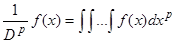 , так как
, так как 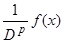 является по определению оператора
является по определению оператора 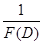 решением уравнения
решением уравнения 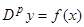 .
.
Проверим следующие свойства оператора 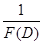 .
.
1) 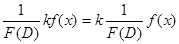 , где
, где  — постоянный множитель, так как
— постоянный множитель, так как 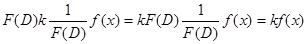 .
.
2) 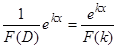 , если
, если 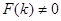 . Действительно,
. Действительно,  является решением уравнения
является решением уравнения 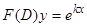 , так как следуя первому свойству оператора
, так как следуя первому свойству оператора 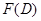 ,
, 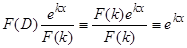 .
.
3) 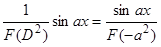 , если
, если  . Действительно,
. Действительно, 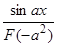 является решением уравнения
является решением уравнения 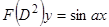 , так как по второму свойству оператора
, так как по второму свойству оператора 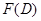 :
: 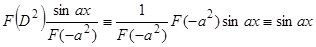 .
.
4) 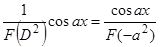 . Доказывается аналогично предыдущему с использованием третьего свойства оператора
. Доказывается аналогично предыдущему с использованием третьего свойства оператора 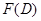 .
.
5) 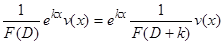 . Действительно,
. Действительно, 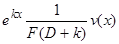 является решением уравнения
является решением уравнения 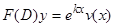 , так как по четвертому свойству оператора
, так как по четвертому свойству оператора 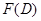 ,
, 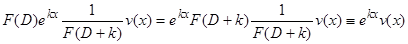 .
.
6) 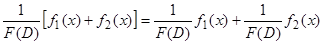 . Это равенство является следствием принципа суперпозиции.
. Это равенство является следствием принципа суперпозиции.
7) 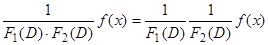 , т.е.
, т.е. 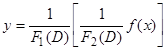 является решением уравнения
является решением уравнения 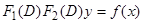 . Подставим предполагаемое решение в это уравнение. Получим
. Подставим предполагаемое решение в это уравнение. Получим 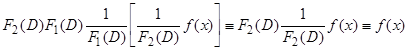 .
.
Приведем несколько примеров нахождения частных решений линейных неоднородных уравнений с постоянными коэффициентами операторным методом.
1) 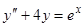 , или
, или 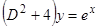 , откуда
, откуда 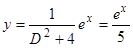 .
.
2) 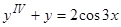 , или
, или 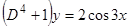 ,
, 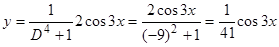 .
.
3) 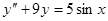 ,
, 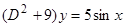 ,
,  .
.
4) 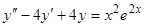 ,
, 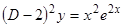 ,
, 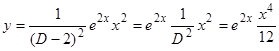 .
.
5)  ,
, 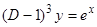 ,
, 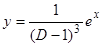 .
. 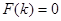 , поэтому вместо второй формулы применяем формулу 5) свойств оператора
, поэтому вместо второй формулы применяем формулу 5) свойств оператора 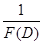 , рассматривая
, рассматривая 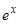 как произведение
как произведение 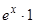 :
: 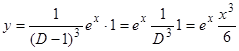 .
.
6) 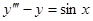 ,
, 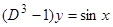 ,
, 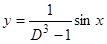 . Так как оператор содержит нечетные степени
. Так как оператор содержит нечетные степени 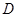 , то воспользоваться формулой 4) свойств оператора
, то воспользоваться формулой 4) свойств оператора 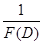 нельзя. Поэтому вместо исходного уравнения рассмотрим уравнение
нельзя. Поэтому вместо исходного уравнения рассмотрим уравнение 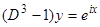 , или
, или 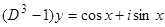 . Мнимая часть решения этого уравнения будет решением исходного уравнения:
. Мнимая часть решения этого уравнения будет решением исходного уравнения: 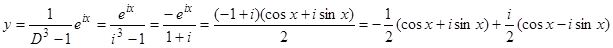 . Мнимая часть решения
. Мнимая часть решения 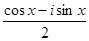 является решением исходного уравнения
является решением исходного уравнения 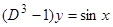 .
.
7) 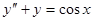 ,
, 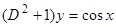 ,
, 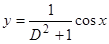 . Формула 3) свойств оператора
. Формула 3) свойств оператора 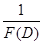 неприменима, т.к.
неприменима, т.к. 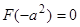 , поэтому опять вместо заданного уравнения рассматриваем уравнение
, поэтому опять вместо заданного уравнения рассматриваем уравнение 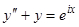 или
или 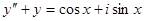 и берем действительную часть его решения
и берем действительную часть его решения  ,
, 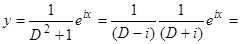
 . Взяв действительную часть найденного решения вспомогательного уравнения
. Взяв действительную часть найденного решения вспомогательного уравнения 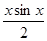 , получим решение исходного уравнения.
, получим решение исходного уравнения.
8) 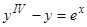 ,
,  ,
, 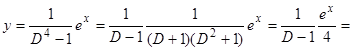
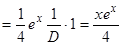 .
.
Выясним еще, как действует оператор 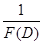 на полином
на полином 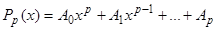 . Формально разделим 1 на полином
. Формально разделим 1 на полином  , расположенный по возрастающим степеням
, расположенный по возрастающим степеням 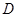 , по правилу деления обычных (не операторных) полиномов. Процесс деления прекратим тогда, когда в частном получим операторный полином степени
, по правилу деления обычных (не операторных) полиномов. Процесс деления прекратим тогда, когда в частном получим операторный полином степени 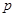 :
:  . При этом в остатке окажется полином
. При этом в остатке окажется полином 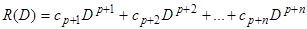 , содержащий оператор
, содержащий оператор 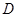 в степенях не ниже
в степенях не ниже 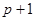 . В силу зависимости между делимым, делителем, частным и остатком получим
. В силу зависимости между делимым, делителем, частным и остатком получим
 . (14)
. (14)
Это тождество справедливо для обычных (не операторных) полиномов, но так как правила сложения и умножения операторных полиномов не отличаются от правил сложения и умножения обычных полиномов, то тождество справедливо и для операторных полиномов. Действуя левой и правой частями тождества (14) на полином 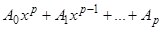 , получим
, получим 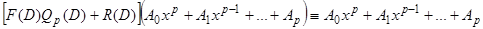 , или, принимая во внимание, что
, или, принимая во внимание, что 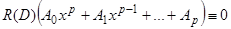 , так как
, так как 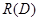 содержит
содержит 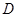 в степенях не ниже
в степенях не ниже 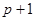 , будем иметь
, будем иметь  , т.е.
, т.е. 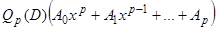 является решением уравнения
является решением уравнения 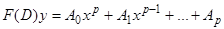 .
.
Итак, 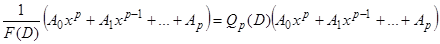 .
.
Например:
9) 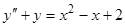 ,
,  ,
, 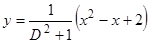 . Разделив 1 на
. Разделив 1 на  , получим
, получим 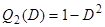 . Следовательно,
. Следовательно, 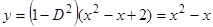 .
.
10) 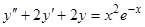 ,
, 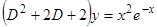 ,
, 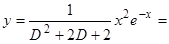
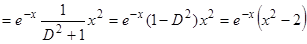 .
.
11) 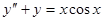 ,
, 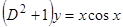 . Перейдем к уравнению
. Перейдем к уравнению 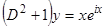 и потом возьмем действительную часть решения
и потом возьмем действительную часть решения 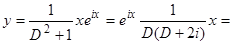
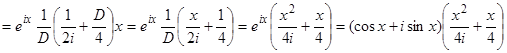 . Взяв действительную часть
. Взяв действительную часть  , получим искомое решение.
, получим искомое решение.
Этот последний пример показывает, как нужно действовать оператором 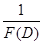 на полином, если
на полином, если 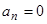 . Представив
. Представив 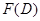 в виде
в виде 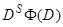 , где свободное слагаемое полинома
, где свободное слагаемое полинома 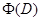 уже не равно нулю, действуем на полином вначале оператором
уже не равно нулю, действуем на полином вначале оператором 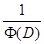 , а затем оператором
, а затем оператором 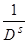 .
.
Неоднородные уравнения Эйлера
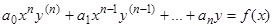 (15)
(15)
или
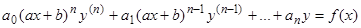 (16)
(16)
можно интегрировать путем решения соответствующих однородных уравнений, которые мы уже рассматривали, и подбора одного частного решения неоднородного уравнения, либо же применяя метод вариации произвольных постоянных. Однако обычно проще вначале проинтегрировать однородное уравнение, а для подбора частного решения преобразовать уравнение Эйлера (15) заменой переменных  (для уравнения (16)
(для уравнения (16) 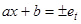 ) к уравнению с постоянными коэффициентами, для которых хорошо разработаны методы нахождения частных решений.
) к уравнению с постоянными коэффициентами, для которых хорошо разработаны методы нахождения частных решений.
Пример 11. 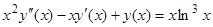 . Ищем решение соответствующего однородного уравнения в виде
. Ищем решение соответствующего однородного уравнения в виде 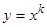 .
. 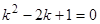 ,
, 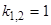 , следовательно, общее решение однородного уравнения имеет вид
, следовательно, общее решение однородного уравнения имеет вид 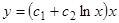 . Заменой переменных
. Заменой переменных 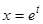 преобразуем исходное уравнение в уравнение с постоянными коэффициентами
преобразуем исходное уравнение в уравнение с постоянными коэффициентами 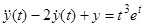 (левая часть этого уравнения может сразу быть написана по характеристическому уравнению, соответствующему исходному). Операторным методом находим частное решение преобразованного уравнения
(левая часть этого уравнения может сразу быть написана по характеристическому уравнению, соответствующему исходному). Операторным методом находим частное решение преобразованного уравнения 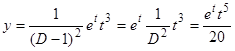 ,
, 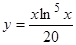 . Следовательно, общее решение исходного уравнения имеет вид
. Следовательно, общее решение исходного уравнения имеет вид 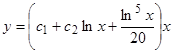 .
.
 2014-02-02
2014-02-02 2920
2920
