Простейшие типы точек покоя

Исследуем расположение траекторий в окрестности точки покоя 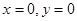системы двух линейных однородных уравнений с постоянными коэффициентами:

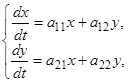(6)

где .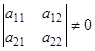

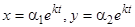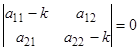Коэффициенты постоянные, поэтому решение ищем в виде . Для определения получаем характеристическое уравнение или 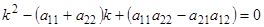. 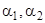с точностью до постоянного множителя определяются из одного из уравнений

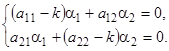(7)

Рассмотрим следующие случаи.

а) Корни характеристического уравнения 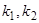действительны и различны.

Общее решение имеет вид

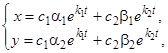(8)

где 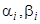— постоянные, определяемые из уравнения (7) соответственно 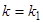при и при 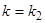, а 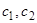— произвольные постоянные.

При этом возможны следующие случаи.

1) Есл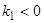и и 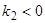, то точка покоя 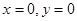асимптотически устойчива, так как из-за наличия множителе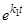й и 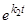в (8) все точки, находящиеся в начальный момент 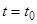в любой 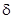-окрестности начала координат, при достаточно большом переходят в точки, лежащие в сколь угодно малой 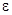-окрестности начала координат, а при 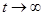стремятся к началу координат. На рис изображено расположение траекторий около точки покоя рассматриваемого типа, называемой устойчивым узлом, причем стрелками указано направление движения по траекториям при возрастании .

2) Пусть . Этот случай переходит в предыдущий при замене на 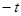. Следовательно, траектории имеют такой же вид, как и в предыдущем случае, но только точка по траекториям движется в противоположном направлении (рис). Очевидно, что с возрастанием точки, сколь угодно близкие к началу координат, удаляются из 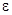-окрестности начала координат — точка покоя неустойчива в смысле Ляпунова. Точка покоя такого типа называется неустойчивым узлом.

3) Если 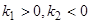, то точка покоя тоже неустойчива, так как движущаяся по траектории

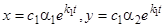(9)

точка при сколь угодно малых значениях 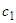с возрастанием выходит из 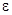-окрестности начала координат.

Заметим, что в рассматриваемом случае существуют движения, приближающиеся к началу координат, а именно 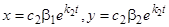. При различных значениях 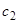получаем различные движения по одной и той же прямой 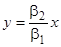. При возрастании точки на этой прямой движутся по направлению к началу координат (рис). Заметим также, что точки траектории (9) движутся с возрастанием по прямой 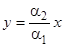, удаляясь от начала координат. Если же 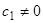и , то как при 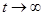, так и при 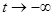траектория покидает окрестность точки покоя.

Точка покоя рассматриваемого типа называется седлом (рис) потому, что расположение траекторий в окрестности такой точки напоминает расположение линий уровня в окрестности седлообразной точки некоторой поверхности .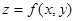

б) Корни характеристического уравнения комплексные: .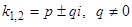

Общее решение рассматриваемой системы можно представить в виде

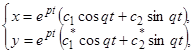(10)

где 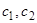— произвольные постоянные, а 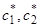— некоторые линейные комбинации этих постоянных.

При этом возможны следующие случаи.

1) .

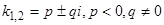Множитель 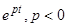, стремится к нулю с возрастанием , а второй — периодический множитель в уравнениях (10) остается ограниченным.

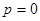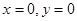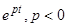Если бы , то траекториями были бы, в силу периодичности вторых множителей в правой части уравнений (10), замкнутые кривые, окружающие точку покоя (рис.). Наличие стремящегося к нулю с возрастанием множителя , превращает замкнутые кривые в спирали, асимптотически приближающиеся при 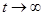к началу координат (рис.), причем при достаточно большом точки, находившиеся при 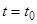в любой 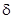-окрестности начала координат, попадают в заданную 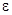-окрестность точки покоя 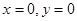, а при дальнейшем возрастании стремятся к точке покоя. Следовательно, точка покоя асимптотически устойчива — она называется устойчивым фокусом. Фокус отличается от узла тем, что касательная к траекториям не стремится к определенному пределу при приближении точки касания к точке покоя.

2) .

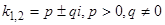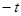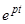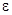Этот случай переходит в предыдущий при замене на . Следовательно, траектории не отличаются от траекторий предыдущего случая, но движение по ним происходит при возрастании в противоположном направлении (рис.). Из-за наличия возрастающего множителя точки, находившиеся в начальный момент сколь угодно близко к началу координат, с возрастанием удаляются из -окрестности начала координат — точка покоя неустойчива. Она носит название неустойчивого фокуса.

3) .

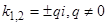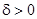Как мы уже отмечали, в силу периодичности решений, траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис.). Центр является устойчивой точкой покоя, так как для заданного можно подобрать такое, что замкнутые траектории, начальные точки которых лежат в 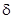-окрестности начала координат, не выходят за пределы 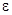-окрестности начала координат или, что то же самое, можно подобрать столь малые 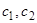, что решения

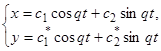(11)

будут удовлетворять неравенству 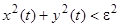. Заметим, однако, что асимптотической устойчивости в рассматриваемом случае нет, так как и в (11) не стремятся к нулю при .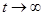

в) Корни кратны .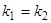

1) .

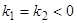Общее решение имеет вид 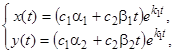причем не исключена возможность того, что 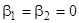, но тогда 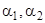будут произвольными постоянными.

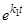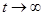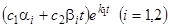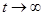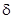Из-за наличия быстро стремящегося к нулю множителя при произведение стремится к нулю при , причем при достаточно большом все точки любой -окрестности начала координат попадают в заданную 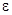-окрестность начала координат и, следовательно, точка покоя асимптотически устойчива. На рис. изображена точка покоя рассматриваемого вида, так же как и в случае а) 1), называемая устойчивым узлом. Этот узел занимает промежуточное положение между узлом а) 1) и фокусом б) 1), так как при сколь угодно малом изменении действительных коэффициентов 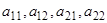он может превратиться как в устойчивый фокус, так и в устойчивый узел типа а) 1), потому что при сколь угодно малом изменениикоэффициентов кратный корень может перейти как в пару комплексных сопряженных корней, так и в пару действительных различных корней. Если 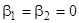, то тоже получаем устойчивый узел (так называемый дикритический узел), изображенный на рис..

2) Если , то замена на 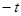приводит к предыдущему случаю. Следовательно, траектории не отличаются от траекторий предыдущего случая, но движение по ним проходит в противоположном направлении. В этом случае точка покоя называется, так же, как и в случае а) 2), неустойчивым узлом.

Тем самым исчерпаны все возможности, так как случа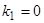й или 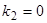исключен условием .

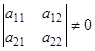Если все же 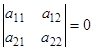, то характеристическое уравнение 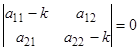имеет нулевой корень 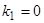. Предположим, что 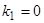, но 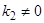. Тогда общее решение системы (6) имеет вид 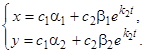Исключая , получим семейство параллельных прямых 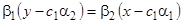. При 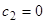получаем однопараметрическое семейство точек покоя, расположенных на прямой 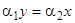. Если 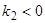, то при 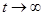на каждой траектории точки приближаются к лежащей на этой траектории точке покоя 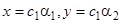(рис.). Точка покоя 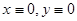устойчива, но асимптотической устойчивости нет.

Если же 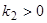, то траектории расположены так же, но движение точек по траекториям происходит в противоположном направлении — точка покоя 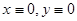неустойчива.

Если же 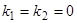, то возможны два случая.

1) Общее решение системы (6) имеет вид 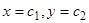— все точки являются точками покоя, все решения устойчивы.

2) Общее решение имеет вид 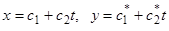, где 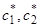— линейные комбинации произвольных постоянных 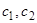. Точка покоя 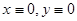неустойчива.

Заметим, что если оба корня характеристического уравнения имеют отрицательную действительную часть (случаи а) 1); б) 1); в) 1)), то точка покоя асимптотически устойчива. Если же хотя бы один корень характеристического уравнения имеет положительную действительную часть (случаи а) 2), б) 2), в) 2)), то точка покоя неустойчива.

Аналогичные утверждения справедливы и для системы 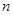линейных однородных уравнений с постоянными коэффициентами

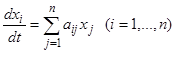. (13)

Если действительные части всех корней характеристического уравнения системы (13) отрицательны, то тривиальное решение 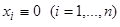асимптотически устойчиво. Если же действительная часть хотя бы одного корня характеристического уравнения положительна, то точка покоя 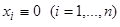системы (13) неустойчива.

Пример 1. Какого типа точку покоя имеет система уравнений ?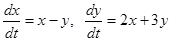

Характеристическое уравнение 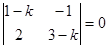или 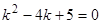имеет корни 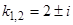, следовательно, точка покоя 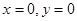является неустойчивым фокусом.

Пример 2. 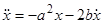— уравнение упругих колебаний с учетом трения или сопротивления среды (при 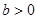). Переходя к эквивалентной системе уравнений, получим 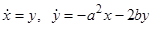. Характеристическое уравнение имеет вид 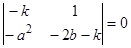или 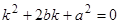, откуда 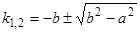. Рассмотрим следующие случаи.

1) 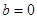, т.е. сопротивление среды не учитывается. Все движения периодические. Точка покоя в начале координат является центром.

2) 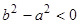, 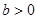. Точка покоя является устойчивым фокусом. Колебания затухают.

3) 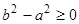, 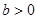. Точка покоя является устойчивым узлом. Все решения затухающие, неколеблющиеся. Этот случай наступает, если сопротивление среды велико ().

4) 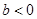(случай отрицательного трения). 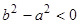. Точка покоя является неустойчивым фокусом.

5) 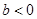, 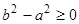(случай большого отрицательного трения). Точка покоя является неустойчивым узлом.

Пример 3. Исследовать на устойчивость точку покоя системы уравнений 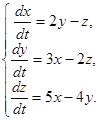Характеристическое уравнение: 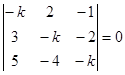, или .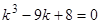

Определить корни кубического уравнения в общем случае довольно трудно, однако в данном случае один корень 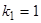легко подбирается и так как этот корень имеет положительную действительную часть, то можно утверждать, что точка покоя 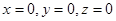неустойчива.