Исследование на устойчивость по первому приближению

При исследовании на устойчивость точки покоя 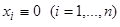системы дифференциальных уравнений

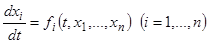, (14)

где 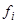— дифференцируемые в окрестности начала координат функции, часто применяется следующий метод: пользуясь дифференцируемостью функций 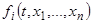, представляют систему (14) в окрестности начала координат 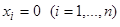в виде

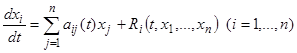, (15)

где 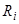имеют порядок выше первого относительно 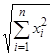, и вместо точки покоя 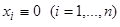системы (15) исследуют на устойчивость ту же точку покоя линейной системы

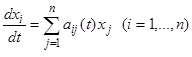, (16)

называемой системой уравнений первого приближения для системы (15). Условия применимости этого метода, которым долгое время пользовались без всякого обоснования, были детально исследованы Ляпуновым и в дальнейшем расширены трудами многих других математиков.

Исследование на устойчивость системы уравнений первого приближения, конечно, является задачей значительно более легкой, чем исследование исходной, вообще говоря, нелинейной системы, однако даже исследование линейной системы (16) при переменных коэффициентах является задачей весьма сложной. Если же все 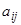постоянны, т.е. система стационарна в первом приближении, то исследование на устойчивость линейной системы (16) не представляет принципиальных затруднений, о чем мы уже говорили в нашей теме.

Теорема 4. Если система уравнений (15) стационарна в первом приближении, все слагаемые 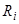в достаточно малой окрестности начала координат при 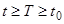удовлетворяют неравенствам 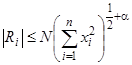, где 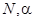— постоянные, причем 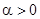(т.е. если 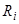не зависят от , то их порядок выше первого относительно 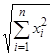) и все корни характеристического уравнения

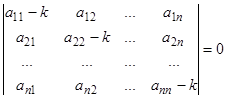(17)

имеют отрицательные действительные части, то тривиальные решения 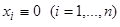системы уравнений (15) и системы уравнений (16) асимптотически устойчивы, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.

Теорема 5. Если система уравнений (15) стационарна в первом приближении, все функции 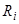удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (17) имеет положительную действительную часть, то точки покоя 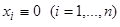системы (15) и системы (16) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по первому приближению.

Теоремы 4 и 5 в отношении ограничений, налагаемых на корни характеристического уравнения, не охватывают лишь так называемый критический случай: все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю.

В критическом случае на устойчивость тривиального решения системы (15) начинают влиять нелинейные слагаемые 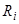и исследование на устойчивость по первому приближению, вообще говоря, невозможно.

Пример 1. Исследовать на устойчивость точку покоя 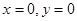системы

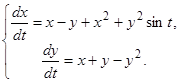(19)

Нелинейные слагаемые удовлетворяют условиям теорем 4 и 5. Исследуем на устойчивость точку покоя 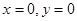системы первого приближения

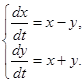(20)

Характеристическое уравнение 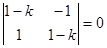имеет корни 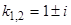, следовательно, в силу теоремы 5 точка покоя систем (19) и (20) неустойчива.

Пример 2. Исследовать на устойчивость точку покоя 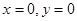системы

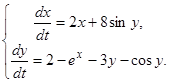(21)

Разлагая 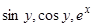по формуле Тейлора, представляем систему в ви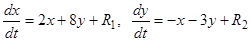де , где 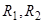удовлетворяют условиям теорем 4 и 5. Характеристическое уравнение 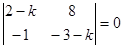для системы первого приближения

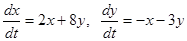(22)

имеет корни с отрицательными действительными частями. Следовательно, точка покоя 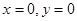систем (21) и (22) асимптотически устойчива.

Пример 3. Исследовать на устойчивость точку покоя 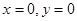системы

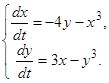(23)

Характеристическое уравнение 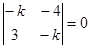для системы первого приближения имеет чисто мнимые корни — критический случай. Исследование по первому приближению невозможно. В данном случае легко подбирается функция Ляпунова .

1) ;

2) 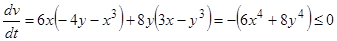, причем вне некоторой окрестности начала координат 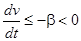, следовательно, точка покоя 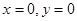по теореме, рассмотренной ранее, асимптотически устойчива.

Остановимся несколько подробнее на последнем примере. Система уравнений первого приближения

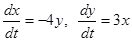(24)

имела в начале координат центр. Наличие нелинейных слагаемых в системе (23) превратило этот центр в устойчивый фокус.

Аналогичная, но несколько более сложная геометрическая картина наблюдается и в общем случае. Пусть система первого приближения для системы

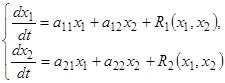(25)

имеет точку покоя типа центра в начале координат. Предположим, как и ранее, что нелинейные слагаемые 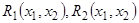имеют порядок выше первого относительно 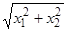. Эти нелинейные слагаемые в достаточно малой окрестности начала координат малы по сравнению с линейными слагаемыми, но все же они несколько искажают поле направлений, определяемое линейной системой первого приближения, поэтому выходящая из некоторой точки 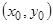траектория после обхода начала координат немного смещается по сравнению с проходящей через ту же точку траекторией линейной системы и, вообще говоря, не попадает в точку 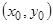— то есть, траектория не замыкается.

Если после такого обхода начала координат все траектории приближаются к началу координат, то в начале координат возникает устойчивый фокус. Если же траектории удаляются от начала координат, возникает неустойчивый фокус.

В виде исключения возможен также случай, при котором все траектории нелинейной системы, расположенные в окрестности начала координат, остаются замкнутыми, однако наиболее типичным надо считать случай, при котором лишь некоторые (может быть, и ни одной) замкнутые кривые остаются замкнутыми, а остальные превращаются в спирали.

Такие замкнутые траектории, в окрестности которых все траектории являются спиралями, называются предельными циклами.

Если близкие к предельному циклу траектории являются спиралями, приближающимися при 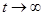к предельному циклу, то предельный цикл называется устойчивым (рис.). Если близкие к предельному циклу траектории являются спиралями, удаляющимися от предельного цикла при 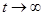, то предельный цикл называется неустойчивым. Если же с одной стороны предельного цикла при 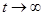спирали приближаются к предельному циклу, а с другой стороны удаляются от него (рис.), то предельный цикл называется полуустойчивым.

Итак, переход от системы первого приближения (16) к системе (25) приводит, вообще говоря, к превращению центра в фокус, окруженный 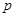(случай 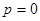не исключается) предельными циклами.

Рассмотрим уравнение

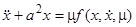. (26)

Заменив его эквивалентной системой, получим

(27)

Соответствующая линейная система имеет в начале координат точку покоя типа центра. Добавление малых при малом 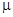нелинейных слагаемых превращает центр, вообще говоря, в фокус, окруженный несколькими предельными циклами. Различие между случаями (25) и (27) заключается лишь в том, что слагаемые 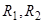малы лишь в достаточно малой окрестности начала координат, тогда как в случае (27) слагаемое 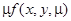может быть сделано малым при достаточно малом 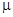не только в достаточно малой окрестности начала координат.

В приложениях устойчивым предельным циклам обычно соответствуют автоколебательные процессы, т.е. периодические процессы, в которых малые возмущения практически не изменяют амплитуды и частоты колебаний.