Теория устойчивости

Лекция 16

Для возможности математического описания какого-либо реального явления неизбежно приходится упрощать, идеализировать это явление, выделяя и учитывая лишь наиболее существенные из влияющих на него факторов и отбрасывая остальные, менее существенные. При этом неизбежно встает вопрос о том, удачно ли выбраны упрощающие предположения. Возможно, что неучтенные факторы сильно влияют на изучаемое явление, значительно меняя его количественные или даже качественные характеристики. В конечном счете этот вопрос решается практикой — соответствием полученных выводов с опытными данными, но все же во многих случаях можно указать условия, при которых некоторые упрощения заведомо невозможны.

Если некоторое явление описывается системой дифференциальных уравнений

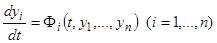(1)

с начальными условиями 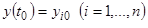, которые обычно являются результатами измерений и, следовательно, неизбежно получены с некоторой погрешностью, то естественно возникает вопрос о влиянии малого изменения начальных значений на искомое решение.

Если окажется, что сколь угодно малые изменения начальных данных способны сильно изменить решение, то решение, определяемое выбранными нами неточными начальными данными, обычно не имеет никакого прикладного значения и даже приближенно не может описывать изучаемое явление.

Следовательно, возникает важный для приложений вопрос о нахождении условий, при которых достаточно малое изменение начальных значений вызывает сколь угодно малое изменение решения.

Если изменяется на конечном отрезке 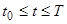, то ответ на этот вопрос дает теорема о непрерывной зависимости решений от начальных значений.

Теорема (о непрерывной зависимости решений от начальных значений). Если правая часть дифференциального уравнения 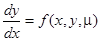непрерывна по 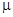при 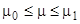и удовлетворяет условиям теоремы существования и единственности в классической формулировке, причем постоянная Липшица 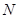не зависит от 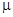, то решение 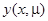рассматриваемого уравнения, удовлетворяющее условию 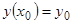, непрерывно зависит от .

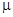Если же может принимать сколь угодно большие значения, то сформулированным вопросом занимается теория устойчивости.

Решение системы (1) называется устойчивым по Ляпунову, если для любого 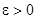можно подобрать 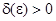такое, что для всякого решения 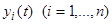той же системы, начальные значения которого удовлетворяют неравенствам 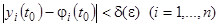, для всех справедливы неравенства

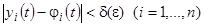, (2)

т.е. близкие по начальным значениям решения остаются близкими для всех .

Заметим, что если система (1) удовлетворяет условиям теоремы о непрерывной зависимости решений от начальных значений, то в определении устойчивости вместо можно писать 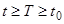, так как в силу этой теоремы на отрезке 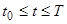решения остаются близкими при достаточно близких начальных значениях.

Если при сколь угодно малом 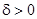хотя бы для одного решения 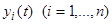неравенства (2) не выполняются, то решение 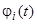называется неустойчивым. Неустойчивые решения лишь в редких случаях представляют интерес в практических задачах.

Если решение не только устойчиво, но, кроме того, удовлетворяет условию

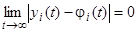, (3)

если 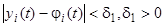, то это решение называется асимптотически устойчивым.

Заметим, что из одного условия (3) еще не следует устойчивость решения .

Пример 1. Исследовать на устойчивость решение дифференциального уравнения 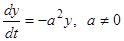, определяемое начальным условием .

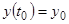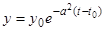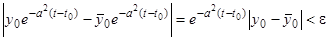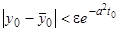Решение асимптотически устойчиво, так как при , если и .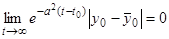

Пример 2. Исследовать на устойчивость решение уравнения 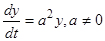, определяемое условием .

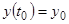Решение 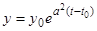неустойчиво, так как нельзя подобрать столь малое 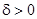, чтобы из неравенства 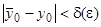следовало бы 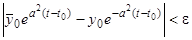или 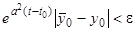при всех .

Исследование на устойчивость некоторого решения системы уравнений (1) может быть сведено к исследованию на устойчивость тривиального решения — точки покоя, расположенной в начале координат.

Действительно, преобразуем систему уравнений (1) к новым переменным, полагая

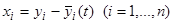. (4)

Новыми неизвестными функциями 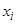являются отклонения 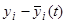прежних неизвестных функций от функций 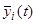, определяющих исследуемое на устойчивость решение.

В силу (4) в новых переменных система (1) принимает вид

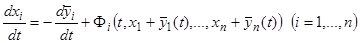. (5)

Очевидно, что исследуемому на устойчивость решению системы (1) в силу зависимости (4) соответствует тривиальное решение 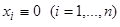системы (5), причем исследование на устойчивость решения системы (1) может быть заменено исследованием на устойчивость тривиального решения системы (5). Поэтому в дальнейшем без ограничения общности можно считать, что на устойчивость исследуется тривиальное решение или, что одно и то же, расположенная в начале координат точка покоя системы уравнений.

Сформулируем условия устойчивости в применении к точке покоя .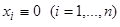

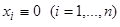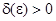Точка покоя системы (5) устойчива в смысле Ляпунова, если для каждого можно подобрать такое, что из неравенства 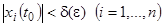следует 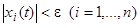при .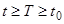

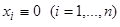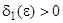Или несколько иначе: точка покоя устойчива в смысле Ляпунова, если для каждого можно подобрать такое, что из неравенства 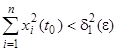следует 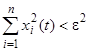при 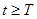, т.е. траектория, начальная точка которой находится в 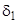-окрестности начала координат при 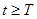не выходит за пределы 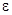-окрестности начала координат.