Лекция 15
Рассмотрим неоднородную систему
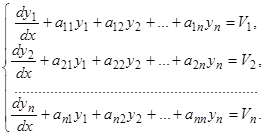 (16)
(16)
Если соответствующие коэффициенты однородной системы
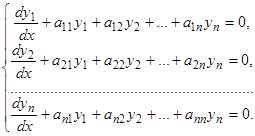 (7)
(7)
равны соответствующим коэффициентам неоднородной системы (16), то однородная система (7) называется соответствующей неоднородной системе (16).
Теорема. Если известно частное решение неоднородной системы: 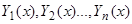 , то нахождение общего решения этой системы приводится к решению соответствующей однородной системы (7).
, то нахождение общего решения этой системы приводится к решению соответствующей однородной системы (7).
В самом деле, введем новые искомые функции 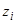 с помощью соотношений
с помощью соотношений 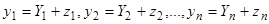 . Подставляя эти выражения в систему (16) и учитывая тождества
. Подставляя эти выражения в систему (16) и учитывая тождества 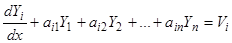 , мы получим для новых функций
, мы получим для новых функций 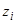 систему
систему
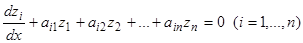 . (7.1)
. (7.1)
Теорема доказана.
Следствие. Общее решение системы (16) имеет вид
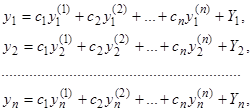
где 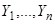 — какое-нибудь частное решение неоднородной системы (16), а
— какое-нибудь частное решение неоднородной системы (16), а
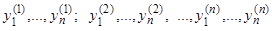 (8)
(8)
есть 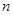 независимых частных решений соответствующей однородной системы (7);
независимых частных решений соответствующей однородной системы (7);  — произвольные постоянные. Доказательство аналогично доказательству соответствующей теоремы для линейного уравнения
— произвольные постоянные. Доказательство аналогично доказательству соответствующей теоремы для линейного уравнения 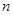 -го порядка.
-го порядка.
Теорема. Если известна фундаментальная система соответствующей однородной системы, то решение неоднородной системы сводится к квадратурам.
Если нам известны решения (8) системы (7), то ее общее решение имеет вид
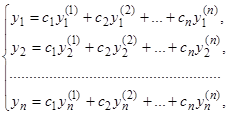 (9)
(9)
где 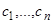 — постоянные. Формулы (9) с постоянными
— постоянные. Формулы (9) с постоянными 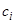 , очевидно, не дают решения неоднородной системы (16). Применим, как и в случае одного линейного уравнения, метод вариации произвольной постоянной. Будем рассматривать
, очевидно, не дают решения неоднородной системы (16). Применим, как и в случае одного линейного уравнения, метод вариации произвольной постоянной. Будем рассматривать 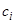 как неизвестные функции от
как неизвестные функции от 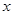 , причем подберем их таким образом, чтобы выражения (9) являлись решениями неоднородной системы (систему уравнений (9) можно рассматривать как систему, вводящую
, причем подберем их таким образом, чтобы выражения (9) являлись решениями неоднородной системы (систему уравнений (9) можно рассматривать как систему, вводящую 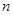 новых искомых функций от
новых искомых функций от 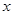 :
: 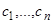 ; в силу линейности преобразования, новые уравнения для
; в силу линейности преобразования, новые уравнения для 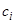 тоже будут линейными).
тоже будут линейными).
Дифференцируем равенства (9) по 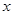 :
:
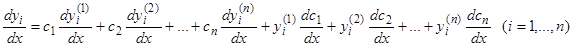 . (17)
. (17)
Подставим выражения (17) и (9) в уравнения (16). Первые 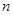 слагаемых правых частей формул (17) имеют такой вид, как если бы
слагаемых правых частей формул (17) имеют такой вид, как если бы 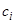 были постоянными. Так как
были постоянными. Так как  представляют собой решения однородной системы, то при подстановке эти слагаемые дадут нули. В самом деле, результат подстановки в
представляют собой решения однородной системы, то при подстановке эти слагаемые дадут нули. В самом деле, результат подстановки в 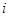 -е уравнение дает
-е уравнение дает
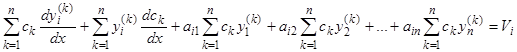 ,
,
или 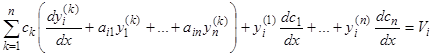 ,
,
и для определения 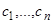 остаются уравнения
остаются уравнения
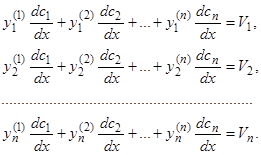
Полученная система линейных уравнений относительно  разрешима, так как определитель системы
разрешима, так как определитель системы 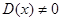 в силу предположения, что система
в силу предположения, что система 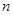 решений (8) является фундаментальной. Мы получаем
решений (8) является фундаментальной. Мы получаем
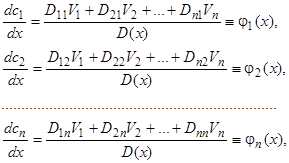
где через 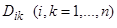 обозначен минор (алгебраическое дополнение) определителя
обозначен минор (алгебраическое дополнение) определителя 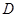 , соответствующий элементу
, соответствующий элементу 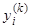 . Так как
. Так как 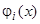 являются известными функциями, то
являются известными функциями, то 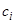 получатся квадратурами
получатся квадратурами 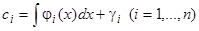 ,
, 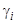 — постоянные интегрирования.
— постоянные интегрирования.
Подставляя найденные значения 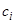 в формулы (9), получаем общее решение системы (16) в виде
в формулы (9), получаем общее решение системы (16) в виде

где частное решение неоднородной системы 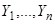 определяется формулами
определяется формулами
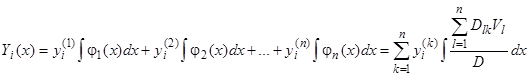 .
.
Рассмотрим еще несколько теорем в сокращенных обозначениях, введенных ранее.
Теорема. Если 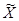 является решением линейной неоднородной системы
является решением линейной неоднородной системы
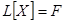 , (*)
, (*)
а 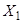 — решением соответствующей однородной системы
— решением соответствующей однородной системы 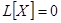 , то сумма
, то сумма 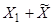 также будет решением неоднородной системы (*).
также будет решением неоднородной системы (*).
Доказательство. Дано, что 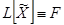 и
и 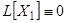 . Надо доказать, что
. Надо доказать, что 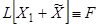 .
.
Пользуясь свойством 2) оператора 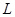 , получим
, получим 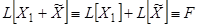 .
.
Теорема (принцип суперпозиции). Решением системы линейных уравнений
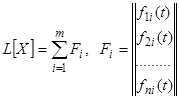
является сумма 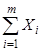 решений
решений 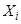 уравнений
уравнений 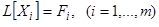 .
.
Доказательство. Дано 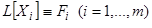 . Надо доказать, что
. Надо доказать, что 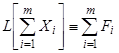 .
.
Используя свойство 2) оператора 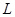 , получим
, получим 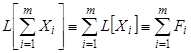 .
.
Теорема. Если система линейных уравнений 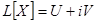 , где
, где 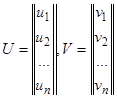 , с действительными функциями
, с действительными функциями 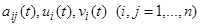 имеет решение
имеет решение 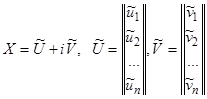 , то действительная часть решения
, то действительная часть решения 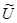 и его мнимая часть
и его мнимая часть 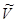 соответственно являются решениями уравнений
соответственно являются решениями уравнений 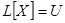 и
и 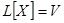 .
.
Доказательство. Дано 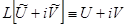 , надо доказать, что
, надо доказать, что  .
.
Пользуясь свойствами 1) и 2) оператора 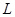 , получаем
, получаем 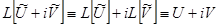 . Следовательно,
. Следовательно,  .
.
Пример. 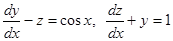 . В примере из прошлой темы мы нашли решение соответствующей однородной системы:
. В примере из прошлой темы мы нашли решение соответствующей однородной системы: 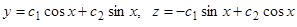 . Подставляем эти значения в данные уравнения, считая
. Подставляем эти значения в данные уравнения, считая 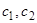 неизвестными функциями от
неизвестными функциями от 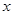 . После приведения получим такую систему:
. После приведения получим такую систему:
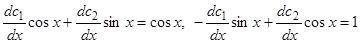 ,
,
откуда, разрешая относительно 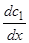 и
и 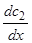 и затем интегрируя, находим
и затем интегрируя, находим
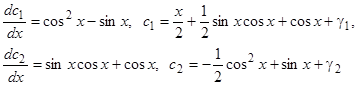
(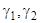 — произвольные постоянные).
— произвольные постоянные).
Подставляя найденные значения 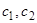 в выражения для
в выражения для 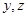 , получаем общее решение исходной неоднородной системы:
, получаем общее решение исходной неоднородной системы:
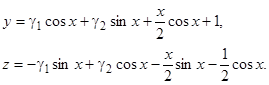
 2014-02-02
2014-02-02 1587
1587
