Первые интегралы системы обыкновенных дифференциальных уравнений

1. Рассмотрим систему уравнений:

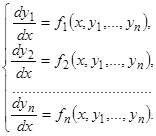(23)

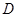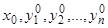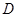Мы предположим, что в некоторой замкнутой области функции и все их частные производные по непрерывно зависят от всех аргументов. Тогда применима теорема существования и единственности. Если точка с координатами лежит внутри некоторой области , содержащейся в , то существует одна и только одна система решений уравнений (23), удовлетворяющих начальным условиям 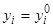при 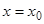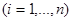. Пусть эти решения будут

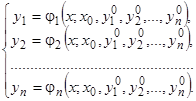(24)

В этих формулах мы явно указываем зависимость решения от начальных данных 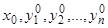, которые мы принимаем за параметры, могущие принимать различные значения.

Рассмотрим теперь в области 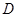начальную точку 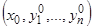и некоторую точку 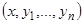, лежащую на интегральной кривой, проходящей через начальную точку. Значения 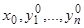, с одной стороны, и значения 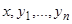, с другой стороны, связаны соотношениями (24). Если теперь принять точку 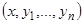за начальную, то, в силу свойства единственности, определенная этими начальными значениями интегральная кривая пройдет через точку 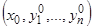, причем, очевидно, будут иметь место соотношения

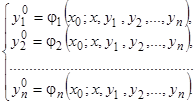(25)

Формулы (25) показывают, что система уравнений (24) может быть разрешена (однозначно в области ) относительно начальных значений .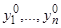

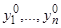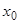Заменяя начальные значения через произвольные постоянные и давая параметру определенное числовое значение, мы получим совокупность уравнений вида

(26)

Совокупность равенств (26) называется общим интегралом системы (23), а каждое из равенств (26) называется первым интегралом этой системы. Заметим, что левая часть каждого из этих равенств есть функция от независимой переменной и искомых функций. Из самого происхождения формул (26) следует, что эта функция обращается в некоторую постоянную величину, если вместо 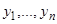подставить их выражения (24), т.е. любое решение системы (23). Очевидно, что для разных решений значение этой постоянной будет, вообще говоря, различное. Таким образом, мы можем дать два определения первого интеграла.

1) Первыми интегралами системы (23) называются соотношения, полученные разрешением уравнений, дающих общее решение системы, относительно произвольных постоянных.

Предыдущее проведенное нами рассуждение показывает, что такое разрешение всегда возможно, если в качестве произвольных постоянных мы возьмем начальные значения искомых функций.

Очевидно, что это определение применимо лишь ко всей системе соотношений (26). Поэтому мы дадим второе определение, характеризующее каждый первый интеграл в отдельности.

2) Первым интегралом системы называется соотношение, не тождественно равное постоянному, содержащее в левой части независимую переменную и искомые функции и принимающее постоянное значение, если вместо искомых функций подставить какое-нибудь решение системы (23).

Заметим, что из этого последнего определения очевидно существование бесконечного множества систем первых интегралов. В самом деле, соотношение

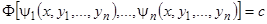, (26.1)

где есть произвольная постоянная, а 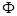— произвольная непрерывная функция своих аргументов, также является первым интегралом системы (23), так как, подставляя вместо 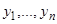решения системы, мы обращаем функции , а следовательно и 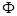, в постоянные величины.

Исходя из второго определения первых интегралов, можно вывести аналитический признак, характеризующий левую часть первого интеграла. Мы его выводить не будем, а просто сформулируем. Итак, предположим, что 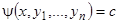— первый интеграл. Пусть в нем на место подставлено какое-нибудь решение системы (23); тогда левая часть обратится в функцию от , тождественно равную постоянной. Равенство 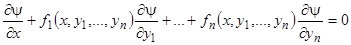есть необходимое и достаточное условие для того, чтобы уравнение 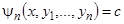представляло собой первый интеграл. В этом равенстве 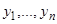— функции от , являющиеся некоторым решением системы (23).

Иногда свойство первого интеграла, выражаемое приведенным равенством, формулируют так: производная от левой части первого интеграла обращается в нуль в силу данной системы дифференциальных уравнений.

Если нам удастся каким-нибудь способом найти независимых первых интегралов системы (23), т.е. таких, которые можно разрешить относительно 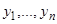, то разрешение их дает выражение 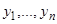через и произвольных постоянных . Эти выражения дадут нам общее решение системы (23).

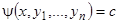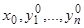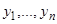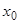В самом деле, условие независимости интегралов вида означает, что якобиан не равен нулю тождественно. Пусть система значений дает ему отличное от нуля значение. Тогда в окрестности этих значений являются однозначными непрерывными функциями от и от . Задавая начальные значения и 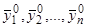в достаточной близости от 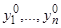и обозначая соответствующие значения постоянных через 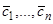, мы видим, что эти значения постоянных определяют решение системы (23): 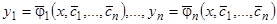, которое при 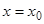принимает наперед заданные значения 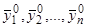. А это и есть критерий для общего решения.

Таким образом, знание (независимых) первых интегралов равносильно интегрированию системы (4).

Если нам известен один первый интеграл системы 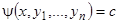, то из него можно выразить одну из искомых функций, например 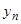, через , остальные искомые функции и произвольную постоянную : 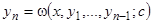. Подставляя это выражение в первое, второе, …, 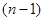-е уравнение системы (23), мы придем к системе 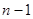уравнений с 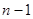искомыми функциями. Таким образом, порядок системы понижается на единицу. Производя интегрирование новой системы 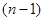-го порядка, мы введем 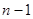произвольных постоянных, которые вместе с дадут систему произвольных постоянных, т.е. мы получили общее решение системы (23). Аналогично, если нам известны независимых первых интегралов, то порядок системы понижается на единиц.

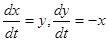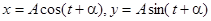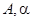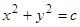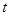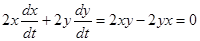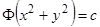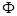Пример. Рассмотрим систему . Ее общее решение есть , где — произвольные постоянные. Очевидно, что соотношение является первым интегралом этой системы. В самом деле, полная производная по от левой части, в силу уравнений системы, будет . Первым интегралом будет также соотношение , где — произвольная дифференцируемая функция.

Пример. В теории движения твердого тела встречается система уравнений 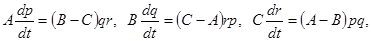где 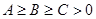— заданные постоянные (главные моменты инерции тела), а искомые функции 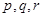— компоненты вектора мгновенной скорости.

Умножая уравнения соответственно на 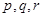и складывая, получим 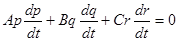. Левая часть есть полный дифференциал. Интегрирование его дает 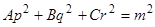(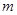— произвольная постоянная) — один первый интеграл уравнения.

Умножая уравнения на 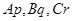и складывая, находим 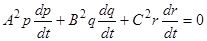, откуда получаем другой первый интеграл 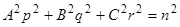(— произвольная постоянная). Других интегралов, не зависимых от этих двух и не содержащих явно 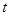, наша система, очевидно, не имеет. По общей теории, мы можем воспользоваться этими интегралами, чтобы понизить порядок системы с третьего до первого. Предполагая 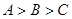, разрешаем два полученных соотношения относительно 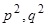. Имеем 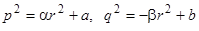, где 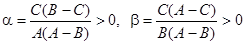, и постоянные величины 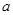и , завися от произвольных постоянных и 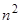, сами являются произвольными.

Подставляя значения 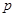и 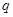в третье уравнение системы, получаем 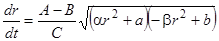. Это уравнение с разделяющимися переменными, и решение получается квадратурой в эллиптических функциях.

Метод, которым мы нашли первые интегралы для этого примера, заключается в том, что мы подбираем такие комбинации левых частей уравнений, которые представляют собой полные производные по 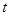, причем правая часть обращается в нуль. Приравнивая соответствующие первообразные функции постоянным, мы получаем первые интегралы.