Выдающийся русский математик Ляпунов в конце XIX века разработал весьма общий метод исследования на устойчивость решения системы дифференциальных уравнений
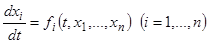 , (14)
, (14)
получивший название второго метода Ляпунова.
Теорема 1 (теорема Ляпунова об устойчивости). Если существует дифференцируемая функция 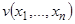 , называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:
, называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:
1)  , причем
, причем 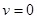 лишь при
лишь при 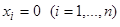 , т.е. функция
, т.е. функция 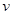 имеет строгий минимум в начале координат;
имеет строгий минимум в начале координат;
2) 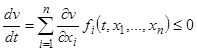 при
при 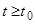 ,
,
то точка покоя 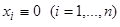 устойчива.
устойчива.
Производная 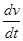 в условии 2) взята вдоль интегральной кривой. Это означает, что она вычислена в предположении, что аргументы
в условии 2) взята вдоль интегральной кривой. Это означает, что она вычислена в предположении, что аргументы 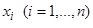 функции
функции 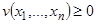 заменены решением
заменены решением  системы дифференциальных уравнений (14). Действительно, в этом предположении
системы дифференциальных уравнений (14). Действительно, в этом предположении 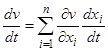 , и заменяя
, и заменяя  правыми частями системы (14), окончательно получим
правыми частями системы (14), окончательно получим 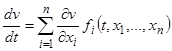 .
.
Теорема 2 (теорема Ляпунова об асимптотической устойчивости). Если существует дифференцируемая функция Ляпунова 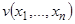 , удовлетворяющая условиям:
, удовлетворяющая условиям:
1) 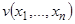 имеет строгий минимум в начале координат:
имеет строгий минимум в начале координат: 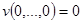 ;
;
2) производная функции 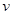 , вычисленная вдоль интегральных кривых системы (14)
, вычисленная вдоль интегральных кривых системы (14) 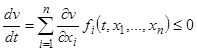 , причем вне сколь угодно малой окрестности начала координат, т.е. при
, причем вне сколь угодно малой окрестности начала координат, т.е. при 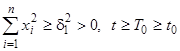 , производная
, производная 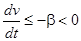 , где
, где 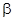 — постоянная, то точка покоя
— постоянная, то точка покоя 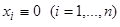 системы (14) асимптотически устойчива.
системы (14) асимптотически устойчива.
Теорема 3 (теорема Четаева о неустойчивости). Если существует дифференцируемая функция 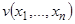 , удовлетворяющая в некоторой замкнутой
, удовлетворяющая в некоторой замкнутой 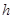 -окрестности начала координат условиям:
-окрестности начала координат условиям:
1) в сколь угодно малой окрестности 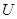 начала координат существует область
начала координат существует область 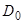 , в которой
, в которой 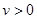 , причем
, причем 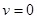 на лежащей в
на лежащей в 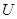 части границы области
части границы области 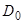 ;
;
2) в области 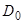 производная
производная 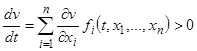 , причем в области
, причем в области 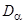 , в которой
, в которой 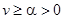 , производная
, производная 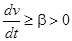 , то точка покоя
, то точка покоя 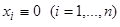 системы (14) неустойчива.
системы (14) неустойчива.
Пример 1. Исследовать на устойчивость тривиальное решение системы 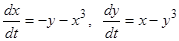 .
.
Берем функцию 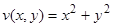 . Она удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости:
. Она удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости:
1)  ;
;
2) 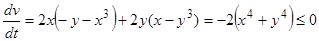 . Вне окрестности начала координат
. Вне окрестности начала координат 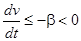 .Следовательно, решение
.Следовательно, решение 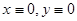 асимптотически устойчиво.
асимптотически устойчиво.
Пример 2. Исследовать на устойчивость тривиальное решение 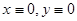 системы
системы 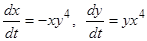 .
.
Функция 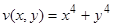 удовлетворяет условиям теоремы Ляпунова об устойчивости:
удовлетворяет условиям теоремы Ляпунова об устойчивости:
1)  ;
;
2) 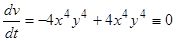 .
.
Следовательно, тривиальное решение 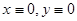 устойчиво.
устойчиво.
Пример 3. Исследовать на устойчивость точку покоя 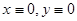 системы уравнений
системы уравнений 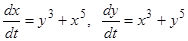 .
.
Функция 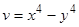 удовлетворяет условиям теоремы Четаева о неустойчивости:
удовлетворяет условиям теоремы Четаева о неустойчивости:
1) 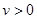 при
при 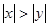 ;
;
2) 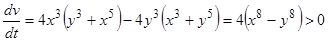 при
при 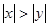 , причем при
, причем при 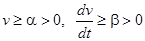 . Следовательно, точка покоя
. Следовательно, точка покоя 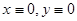 неустойчива.
неустойчива.
Пример 4. Исследовать на устойчивость тривиальное решение 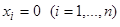 системы уравнений
системы уравнений 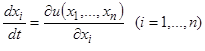 , если дано, что функция
, если дано, что функция 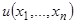 имеет строгий максимум в начале координат.
имеет строгий максимум в начале координат.
В качестве функции Ляпунова возьмем разность 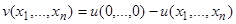 , которая, очевидно, обращается в нуль при
, которая, очевидно, обращается в нуль при 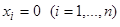 , имеет строгий минимум в начале координат и, следовательно, удовлетворяет условию 1) теоремы Ляпунова об устойчивости. Производная вдоль интегральных кривых
, имеет строгий минимум в начале координат и, следовательно, удовлетворяет условию 1) теоремы Ляпунова об устойчивости. Производная вдоль интегральных кривых 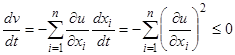 . Итак, условия теоремы Ляпунова об устойчивости выполнены, следовательно, тривиальное решение устойчиво.
. Итак, условия теоремы Ляпунова об устойчивости выполнены, следовательно, тривиальное решение устойчиво.
Пример 5. Исследовать на устойчивость тривиальное решение 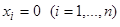 системы уравнений
системы уравнений 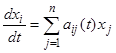 , где
, где 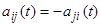 при
при 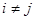 и все
и все 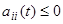 .
.
Тривиальное решение устойчиво, так как функция  удовлетворяет условиям теоремы Ляпунова об устойчивости:
удовлетворяет условиям теоремы Ляпунова об устойчивости:
1) 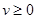 и
и 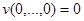 ;
;
2) 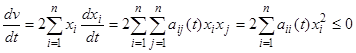 .
.
 2014-02-02
2014-02-02 3540
3540








