Рассмотрим однородную линейную систему
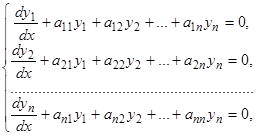 (18)
(18)
в которой будем предполагать коэффициенты 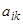 постоянными. Если систему (18) привести к одному уравнению высшего порядка, то получится линейное уравнение с постоянными коэффициентами. Поэтому естественно искать решения системы (18) в виде показательных функций. Будем искать частное решение в таком виде:
постоянными. Если систему (18) привести к одному уравнению высшего порядка, то получится линейное уравнение с постоянными коэффициентами. Поэтому естественно искать решения системы (18) в виде показательных функций. Будем искать частное решение в таком виде:
 (19)
(19)
где 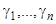 и
и 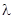 — постоянные, которые нужно определить так, чтобы выражения (19) удовлетворяли системе (18). Подставляя в систему (18) значения (19), сокращая на
— постоянные, которые нужно определить так, чтобы выражения (19) удовлетворяли системе (18). Подставляя в систему (18) значения (19), сокращая на 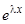 т собирая коэффициенты при
т собирая коэффициенты при 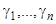 , получим систему алгебраических уравнений
, получим систему алгебраических уравнений
 (20)
(20)
Рассматривая (20) как систему  линейных однородных уравнений относительно
линейных однородных уравнений относительно 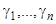 , мы замечаем, что для получения нетривиального решения (19) мы должны потребовать равенства нулю определителя системы (20), т.е. мы приходим к уравнению
, мы замечаем, что для получения нетривиального решения (19) мы должны потребовать равенства нулю определителя системы (20), т.е. мы приходим к уравнению
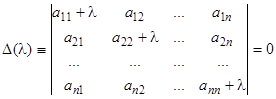 . (21)
. (21)
Наряду с определителем 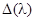 нам в дальнейшем придется часто рассматривать матрицу
нам в дальнейшем придется часто рассматривать матрицу  , составленную из тех же элементов:
, составленную из тех же элементов:
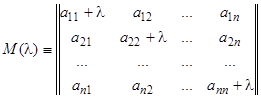 . (21.1)
. (21.1)
Придавая переменной 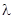 значение
значение 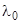 , мы получим матрицу
, мы получим матрицу 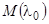 .
.
Уравнение (21) есть уравнение  -й степени относительно
-й степени относительно 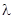 . Мы будем называть его характеристическим уравнением. Итак, решение вида (19) системы (18) может существовать только в том случае, когда
. Мы будем называть его характеристическим уравнением. Итак, решение вида (19) системы (18) может существовать только в том случае, когда 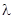 есть корень характеристического уравнения. Могут возникнуть два случая.
есть корень характеристического уравнения. Могут возникнуть два случая.
1). Все  корней характеристического уравнения различны. Пусть эти корни будут
корней характеристического уравнения различны. Пусть эти корни будут 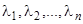 . Если один из этих корней
. Если один из этих корней 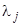 подставить в
подставить в 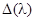 , то мы получим
, то мы получим  . Покажем, что по крайней мере один из миноров (алгебраических дополнений)
. Покажем, что по крайней мере один из миноров (алгебраических дополнений) 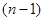 -го порядка определителя
-го порядка определителя 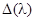 отличен от нуля при
отличен от нуля при 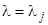 . В самом деле, так как
. В самом деле, так как 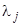 есть простой корень уравнения (21), то
есть простой корень уравнения (21), то 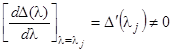 . Вычисляем
. Вычисляем 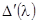 :
:
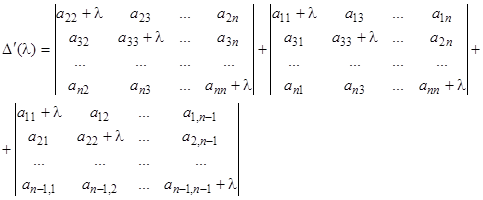
(в правой части стоит сумма диагональных миноров 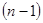 -го порядка).
-го порядка).
Подставляя вместо 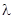 значение
значение  и вспоминая, что
и вспоминая, что 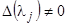 , мы получаем в результате, что по крайней мере один из входящих в последнюю сумму диагональных миноров
, мы получаем в результате, что по крайней мере один из входящих в последнюю сумму диагональных миноров 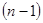 -го порядка не равен нулю при
-го порядка не равен нулю при 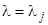 . Наше утверждение доказано.
. Наше утверждение доказано.
Возвращаемся к системе (20), в которой вместо 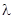 подставим
подставим  — один из корней характеристического уравнения. Определитель системы равен нулю; следовательно, система имеет отличные от нуля решения
— один из корней характеристического уравнения. Определитель системы равен нулю; следовательно, система имеет отличные от нуля решения 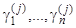 . Но, по доказанному, ранг матрицы
. Но, по доказанному, ранг матрицы 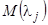 коэффициентов системы (20) равен
коэффициентов системы (20) равен 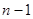 ; следовательно, неизвестные
; следовательно, неизвестные 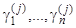 определяются с точностью до произвольного множителя пропорциональности (в качестве
определяются с точностью до произвольного множителя пропорциональности (в качестве 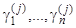 можно взять миноры любой строки определителя
можно взять миноры любой строки определителя 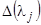 , для которой они не все равны нулю).
, для которой они не все равны нулю).
Итак, мы получим (обозначая этот множитель через  ):
): 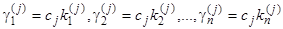 , где
, где 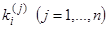 суть известные числа. То есть, корню
суть известные числа. То есть, корню 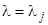 соответствует частное решение системы (18) (мы полагаем
соответствует частное решение системы (18) (мы полагаем 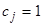 )
)
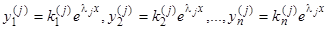 . (22)
. (22)
Ясно значение множителя  : мы знаем, что если систему частных решений домножить на одну и ту же произвольную постоянную, то получим опять решение системы однородных линейных уравнений. Применяя приведенные рассуждения ко всем корням
: мы знаем, что если систему частных решений домножить на одну и ту же произвольную постоянную, то получим опять решение системы однородных линейных уравнений. Применяя приведенные рассуждения ко всем корням 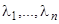 характеристического уравнения, мы получим
характеристического уравнения, мы получим  частных решений вида (22) для
частных решений вида (22) для 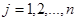 .
.
После этого мы можем записать полное решение системы (18) в виде

Если коэффициенты уравнения действительны, а некоторые корни характеристического уравнения окажутся мнимыми, то они будут входить попарно сопряженными, например:  . Соответствующие решения будут иметь вид
. Соответствующие решения будут иметь вид 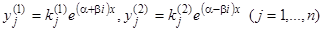 . Коэффициенты
. Коэффициенты 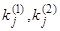 тоже окажутся комплексными сопряженными, если взять их равными минорам одной и той же строки определителей
тоже окажутся комплексными сопряженными, если взять их равными минорам одной и той же строки определителей 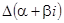 и
и  . Легко убедиться в том, что корням
. Легко убедиться в том, что корням  будут соответствовать две системы решений, соответствующих действительной и мнимой части
будут соответствовать две системы решений, соответствующих действительной и мнимой части 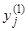 и
и 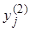 , вида
, вида 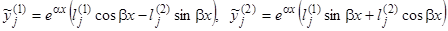 , где
, где 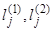 — действительные числа, определяемые из равенств
— действительные числа, определяемые из равенств 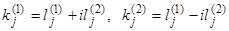 .
.
Пример. 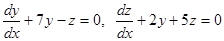 . Ищем решение в виде
. Ищем решение в виде  . Подставляя в заданную систему, получаем уравнения
. Подставляя в заданную систему, получаем уравнения 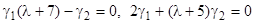 . Условие их совместности дает характеристическое уравнение
. Условие их совместности дает характеристическое уравнение 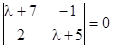 , или
, или 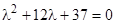 . Корни характеристического уравнения:
. Корни характеристического уравнения: 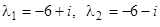 . Подставляя первый из этих корней в систему для определения
. Подставляя первый из этих корней в систему для определения 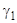 и
и 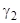 , получаем два уравнения:
, получаем два уравнения: 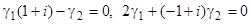 , из которых одно является следствием другого. Мы можем взять
, из которых одно является следствием другого. Мы можем взять 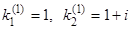 . Первая система частных решений есть
. Первая система частных решений есть 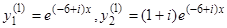 . Аналогично, подставляя корень
. Аналогично, подставляя корень 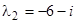 , найдем вторую систему частных решений:
, найдем вторую систему частных решений: 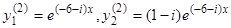 . Беря в качестве новой фундаментальной системы решения
. Беря в качестве новой фундаментальной системы решения 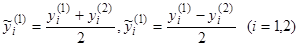 , находим
, находим 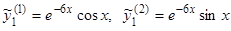 ;
; 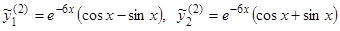 . Общим решением будет
. Общим решением будет  .
.
Заметим, что полученные нами  решений (22) являются линейно независимыми (это можно доказать, но мы не будем).
решений (22) являются линейно независимыми (это можно доказать, но мы не будем).
2). Среди корней уравнения (21) есть кратные. Пусть  есть
есть 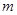 -кратный корень характеристического уравнения. В таком случае значение
-кратный корень характеристического уравнения. В таком случае значение 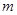 -й производной от
-й производной от 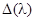 при
при  ,
, 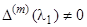 , и рассуждение, аналогичное предыдущему, показывает, что среди миноров порядка
, и рассуждение, аналогичное предыдущему, показывает, что среди миноров порядка 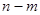 определителя
определителя 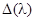 по крайней мере один отличен от нуля при
по крайней мере один отличен от нуля при 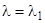 . Отсюда следует, что для ранга
. Отсюда следует, что для ранга 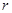 матрицы
матрицы  при
при 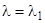 имеет место неравенство
имеет место неравенство 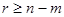 . Система линейных алгебраических уравнений (20) сводится к
. Система линейных алгебраических уравнений (20) сводится к 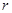 независимым уравнениям. Из теории линейных уравнений известно, что в этом случае в общем решении системы (20)
независимым уравнениям. Из теории линейных уравнений известно, что в этом случае в общем решении системы (20) 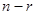 неизвестных остаются произвольными. Пусть это будут
неизвестных остаются произвольными. Пусть это будут 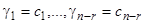 . Остальные
. Остальные 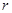 неизвестных
неизвестных 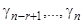 выразятся в виде линейных комбинаций относительно
выразятся в виде линейных комбинаций относительно 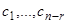 . Пусть эти выражения будут
. Пусть эти выражения будут 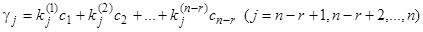 . Мы получим такую систему решений, зависящую от
. Мы получим такую систему решений, зависящую от 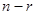 произвольных постоянных
произвольных постоянных 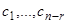 :
:
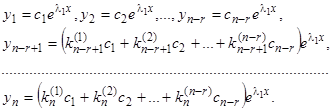
Таким образом, одному корню 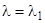 кратности
кратности 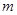 соответствует
соответствует  частных решений, которые мы получаем, полагая
частных решений, которые мы получаем, полагая 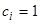 для
для  , а все прочие
, а все прочие  равными нулю (
равными нулю (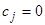 при
при  ):
):
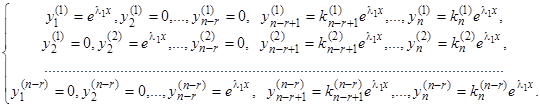 (22.1)
(22.1)
Матрица из коэффициентов при 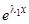 в правых частях этих равенств имеет вид
в правых частях этих равенств имеет вид
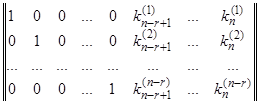 .
.
Ее ранг, очевидно, и равен 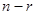 , т.е. между строками системы (22.1) нет линейной зависимости. Значит, мы получили систему
, т.е. между строками системы (22.1) нет линейной зависимости. Значит, мы получили систему 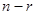 линейно независимых решений, соответствующих корню
линейно независимых решений, соответствующих корню 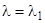 . Если
. Если 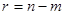 , т.е. если ранг матрицы
, т.е. если ранг матрицы  при
при 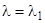 имеет наименьшее значение, то полученное число решений равно кратности
имеет наименьшее значение, то полученное число решений равно кратности 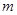 корня
корня  , и, таким образом, получены все решения, соответствующие этому корню (если
, и, таким образом, получены все решения, соответствующие этому корню (если 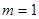 , то
, то 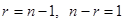 , и мы возвращаемся к случаю простого корня
, и мы возвращаемся к случаю простого корня  , которому соответствует одно решение системы).
, которому соответствует одно решение системы).
Если ранг 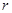 матрицы
матрицы  больше
больше 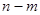 , то число
, то число 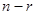 полученных рассмотренным способом решений будет меньше кратности
полученных рассмотренным способом решений будет меньше кратности 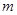 корня
корня  . Чтобы найти недостающие решения, мы должны, как в случае одного уравнения
. Чтобы найти недостающие решения, мы должны, как в случае одного уравнения  -го порядка, искать решения в виде линейных комбинаций функций
-го порядка, искать решения в виде линейных комбинаций функций 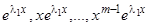 .
.
Пример. 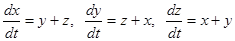 . Ищем решение в форме
. Ищем решение в форме 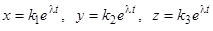 . Для определения
. Для определения 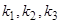 имеем три уравнения:
имеем три уравнения:
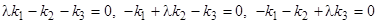 . Приравнивая их определитель нулю, получаем
. Приравнивая их определитель нулю, получаем
 .
.
Корни последнего уравнения суть 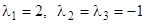 . Простому корню
. Простому корню 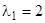 соответствует система двух независимых уравнений для
соответствует система двух независимых уравнений для 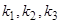 , например
, например 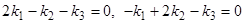 , откуда
, откуда
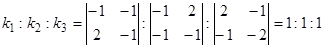 .
.
Отсюда получаем первую систему решений, содержащую одну произвольную постоянную: 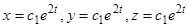 .
.
Если в матрицу  вставить
вставить 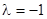 , то ее ранг окажется равным 1, и три уравнения для определения
, то ее ранг окажется равным 1, и три уравнения для определения 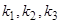 сведутся к одному:
сведутся к одному: 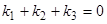 . Если мы положим
. Если мы положим 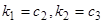 , то
, то 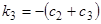 , и мы получим еще систему решений с двумя произвольными постоянными.
, и мы получим еще систему решений с двумя произвольными постоянными.
Общим решением будет 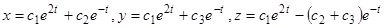 . Мы получили фундаментальную систему решений, так как определитель
. Мы получили фундаментальную систему решений, так как определитель
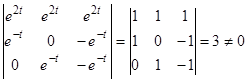 .
.
 2014-02-02
2014-02-02 1230
1230
