Метод Лагранжа нахождения решения д.у.
Теорема.
y oн = y oo + y чн.
Доказательство. Пусть y чн: Ln [ y чн]= f.
а) пусть y *: Ln [ y *]= 0. Рассмотрим y 1 = y * + y чн,
Þ
Ln [ y 1]= Ln [ y * + y чн]= Ln [ y *] + Ln [ y чн]= 0 + f = f;
б) пусть y 1 : Ln [ y 1]= f. Представим его виде
y 1 = (y 1 – y чн) + y чн
и покажем, что функция (y 1 – y чн) Î y oo:
Ln [ y 1 – y чн]= Ln [ y 1] – Ln [ y чн]= f – f = 0.
Замечание. Принцип суперпозиции.
Если f (x) = f 1(x) + f 2(x), то частное решение д. у.
Ln [ y ]= f можно искать в виде
y чн = y чн,1 + y чн,2 ,
где Ln [ y чн,1]= f 1, Ln [ y чн,2]= f 2.
Ln [ y ]= f
Ln [ y ]= 0
(метод вариации произвольных постоянных).
Теорема. Если
y oo = С 1 y 1 + С 2 y 2 + … + Сnyn,
то y чн может быть найдено в виде
y чн = С 1(x) y 1 + С 2(x) y 2 + … + Сn (x) yn, (*)
где С 1(x), С 2(x), …, Сn (x) – непрерывно дифференцируемые функции, подлежащие определению.
n = 2: y oo = С 1 y 1 + С 2 y 2
y чн = С 1(x) y 1 + С 2(x) y 2 (*)
Доказательство (n = 2).
Подставим (*) в уравнение L 2[ y ]= f, т.е.
y ¢¢+ p 1(x) y ¢ + p 2(x) y = 0,
принимая меры для того, чтобы С 1(x), С 2(x), …, Сn (x) входили в него с производными не выше 1-го порядка:
y ¢ = С 1¢ y 1 + С 1 y 1¢ + С 2¢ y 2+ С 2 y 2¢ =
= С 1 y 1¢ + С 2 y 2¢
(если положить С 1¢ y 1 + С 2¢ y 2= 0),
y ¢¢ = С 1¢ y 1¢ + С 1 y 1¢¢ + С 2¢ y 2¢+ С 2 y 2¢¢
L 2[ y ]= С 1¢ y 1¢+ С 2¢ y 2¢+ С 1 (y 1¢¢+ p 1(x) y 1¢+ p 2 (x) y 1) +
+ С 2(y 2¢¢ + p 1(x) y 2¢+ p 2 (x) y 2) = f (x).
Но L 2 [ y 1]= 0, L 2 [ y 2]= 0 Þ
L 2 [ y ]= С 1¢ y 1¢ + С 2 ¢ y 2 ¢ = f (x).
Þ система двух линейных алгебраических уравнений с двумя неизвестными С 1¢, С 2¢:
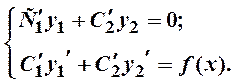
 2014-02-02
2014-02-02 866
866








