Основной определитель

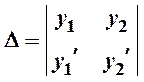
– вронскиан W ₂(x) ¹ 0, т.к. y ₁, y ₂линейно независимы.

Система имеет единственное решение С ₁¢(x), С ₂¢(x).

При любом n:

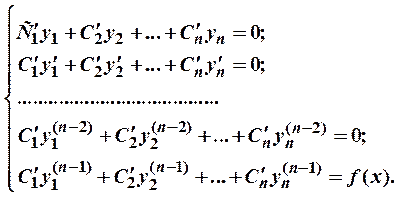
Система имеет единственное решение С ₁¢(x), С ₂¢(x), …, С_n ¢(x).

Интегрируем и подставляем в (*). Ищем частное решение Þ первообразные берем по одной.

Замечание. Если брать все первообразные (с учётом всех произвольных постоянных), то при подстановке в (*) получим не частное, а общее решение уравнения L_n [ y ]= f.

Пример.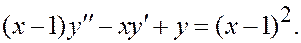

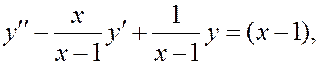(x ¹ 1).

y _oн = y _oo + y _чн.

Соответствующее линейное однородное уравнение:

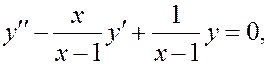y _oo = С ₁ y ₁ + С ₂ y ₂,

y ₁, y ₂ – линейно независимые решения, С ₁, С ₂ – произвольные постоянные.

Легко проверить: y ₁(x) = x и y ₂(x) = e^x – линейно независимые решения.

y _oo = С ₁ x + С ₂ e^x.

Метод вариации: y = С ₁(x) x + С ₂(x) e^x,

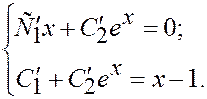
С ₁¢ = –1, С ₂¢ = xe ^{– x}; С ₁(x) = – x, С ₂(x) = – xe ^{– x} – e ^{– x}.

y _чн = (– x) x + (– xe ^{– x} – e ^{– x} ) e^x = – (x ² + x +1),

y _он = С ₁ x + С ₂ e^x – (x ² + x +1).

Замечание. Если С ₁(x) = – x + C ₁, С ₂(x) = – xe ^{– x} – e ^{– x} + C ₂,

то

y = (– x + C ₁) x + (– xe ^{– x} – e ^{– x} + C ₂) e^x =

= С ₁ x + С ₂ e^x – (x ² + x +1) = y _он