Доказательство. где хотя бы одно из чисел a1, a2, , ak ¹ 0

1. Пусть y ₁, y ₂, y_k линейно зависимы. Тогда $ линейная комбинация, тождественно равная нулю:

a₁ y ₁ + a₂ y ₂ + … + a _ky_k º 0,

где хотя бы одно из чисел a₁, a₂, …, a _k ¹ 0.

Дифференцируя (n –1) раз, получим систему

Т. е.

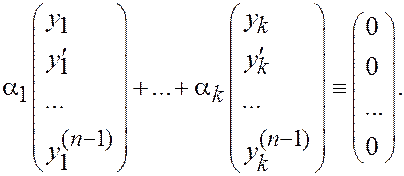
Þ Столбцы начальных условий (как векторы) линейно зависимы (" точки x ₀).

2. Пусть линейно зависимы столбцы начальных условий задач Коши для y ₁, y ₂, y_k:

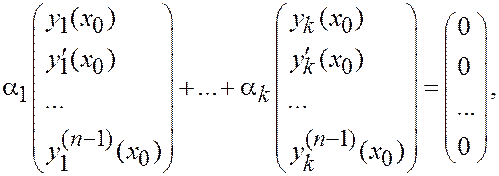
не все a₁, a₂, …, a _k нулевые.

Составим функцию y = a₁ y ₁ + a₂ y ₂ + … + a _ky_k, это – решение. Для него условия задачи Коши в т. x ₀:

.

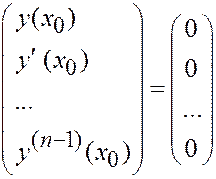Такие же условия для решения y º 0.

Из единственности:

a₁ y ₁ + a₂ y ₂ + … + a _ky_k º 0,

т.е. y ₁, y ₂, y_k линейно зависимы.

Теорема 3 (о структуре общего решения уравнения L_n [ y ]=0). Пространство решений уравнения L_n [ y ]=0 имеет размерность n, т.е.

y _oo = С ₁ y ₁ + С ₂ y ₂ + … + С_ny_n,

где y _oo – общее решение, y ₁, y ₂, y_n – линейно независимые частные решения, базис пространства решений (фундаментальная система решений).

Доказательство. Выберем любые n линейно независимых столбцов, поставим в т. x ₀ n задач Коши, их решения y ₁, y ₂, …, y_n линейно независимы.

Рассмотрим другое решение y_{n +1}.

Для него столбец начальных условий будет линейной комбинацией ранее выбранных n столбцов (длины n).

По теореме 2 y ₁, y ₂, y_n, y_{n +1} линейно зависимы:

y_{n +1} = С ₁ y ₁ + С ₂ y ₂ + … + С_ny_n.