Возведение комплексных чисел в степень

Пример 9.

Возвести в квадрат комплексное число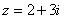

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей 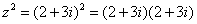и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :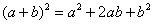

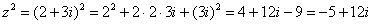
Для комплексного числа легко вывести свою формулу сокращенного умножения:
.

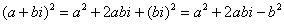Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности.

Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень?

З необходимо использовать тригонометрическую форму комплексного числа и, так называемую, формулу Муавра:

Если комплексное число представлено в тригонометрической форме 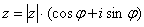, то при его возведении в натуральную степень 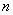справедлива формула:

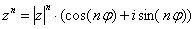
Пример 12

Возвести в степень комплексные числа , ,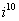

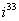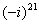
Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то:

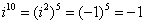
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:

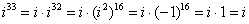
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

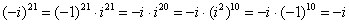
8.5.Извлечение корней из комплексных чисел.
Квадратное уравнение с комплексными корнями

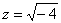
два корня:

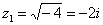
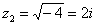
Часто используется сокращенная запись, оба корня записывают в одну строчку: .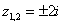

Такие корни также называют сопряженными комплексными корнями.

Корни извлекаются соответствующим образом:

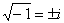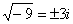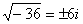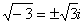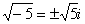, , , , и т.д.

Во всех случаях получается два сопряженных комплексных корня.

Задание на Дом:

РЕШИТЬ ЗАДАЧИ (для тех, кто не был на первой лекции и не делал домашнее задание):