Интегралы типа 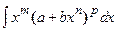 , где a, b – действительные числа, m, n, p – рациональные числа.
, где a, b – действительные числа, m, n, p – рациональные числа.
Подынтегральное выражение  называют дифференциальным биномом.
называют дифференциальным биномом.
Данный интеграл выражается в конечном виде (т.е. первообразная представляет собой элементарную функцию) лишь в следующих трех случаях (этот результат получен выдающимся русским математиком и механиком Пафнутием Львовичем Чебышёвым (1821 – 1894):
1) если p – целое число, то применяется подстановка 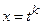 , где k – наименьшее общее кратное знаменателей дробей m и n;
, где k – наименьшее общее кратное знаменателей дробей m и n;
2) если 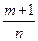 – целое число. Тогда применяется подстановка
– целое число. Тогда применяется подстановка  , где
, где 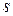 – знаменатель дроби
– знаменатель дроби  ;
;
3) если  – целое число. В этом случае используется подстановка
– целое число. В этом случае используется подстановка  , где
, где 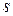 – знаменатель дроби p.
– знаменатель дроби p.
Пример 4. Вычислить 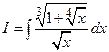 .
.
Решение: Перепишем исходный интеграл  .
.
Это интеграл от дифференциального бинома, где  ;
;  . Следовательно, имеет место случай 2) интегрируемости.
. Следовательно, имеет место случай 2) интегрируемости.
Подстановка  дает:
дает: 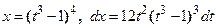 .
.
Поэтому, 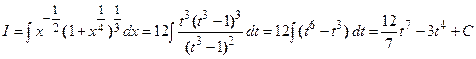 ,
,
где 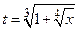 .
.
 2014-02-02
2014-02-02 5362
5362








