Использование тригонометрических преобразований
Интегралы типа 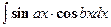 ,
, 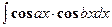 ,
, 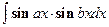 вычисляются с помощью известных формул тригонометрии:
вычисляются с помощью известных формул тригонометрии:
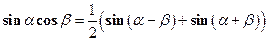
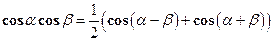
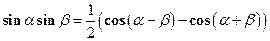
- Квадратичные иррациональности
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
Интегралы типа 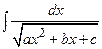 ,
, 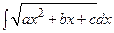 ,
, 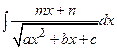 называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат
называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат 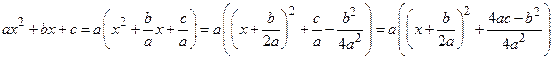 и сделать подстановку
и сделать подстановку 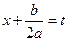 . При этом два первые интеграла приводятся к табличным, а третий – к сумме двух табличных интегралов.
. При этом два первые интеграла приводятся к табличным, а третий – к сумме двух табличных интегралов.
Пример 1. Найти интеграл 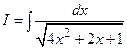 .
.
Решение: Так как 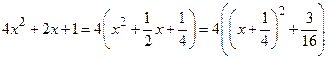 , то
, то 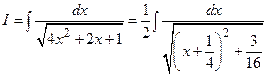 . Сделаем подстановку
. Сделаем подстановку 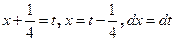 . Тогда
. Тогда 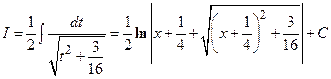 .
.
Пример 2. Найти интеграл 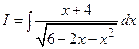 .
.
Решение: Тек как 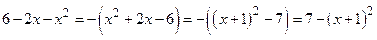 , то подстановка имеет вид
, то подстановка имеет вид 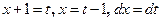 .
.
Тогда,
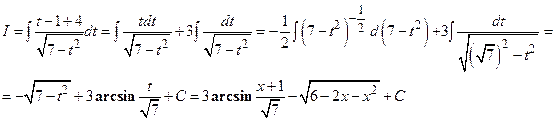 .
.
Интегралы типа 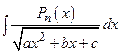 , где
, где 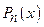 - многочлен степени n, можно вычислять, пользуясь формулой
- многочлен степени n, можно вычислять, пользуясь формулой 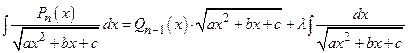 , где
, где 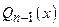 - многочлен степени
- многочлен степени 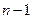 с неопределенными коэффициентами, l - также неопределенный коэффициент.
с неопределенными коэффициентами, l - также неопределенный коэффициент.
Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства
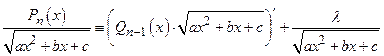 , после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной x.
, после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной x.
2. Дробно – линейная подстановка
Интегралы типа 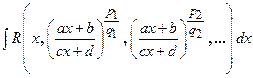 , где
, где 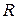 – рациональная функция, a, b, c, d – действительные числа,
– рациональная функция, a, b, c, d – действительные числа, 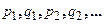 – натуральные числа.
– натуральные числа.
Интегралы такого вида вычисляются с помощью подстановки
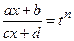 ,
,
где n – общий знаменатель дробей 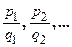 (наименьшее общее кратное чисел
(наименьшее общее кратное чисел 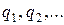 ). В результате этой подстановки подынтегральная функция преобразуется в рациональную.
). В результате этой подстановки подынтегральная функция преобразуется в рациональную.
Пример 3. Вычислить 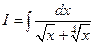 .
.
Решение: Положим 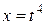 ; тогда
; тогда 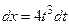 и
и
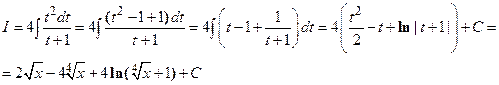
 2014-02-02
2014-02-02 6477
6477








