2014-02-02
796
Пусть функция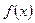 
определена на отрезке 
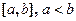. Выполним следующие действия.
1. С помощью точек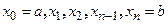 
(
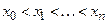) разобьем отрезок 
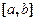на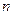 
частичных отрезков 
.
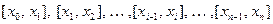2. В каждом частичном отрезке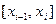 
, 
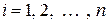выберем произвольную точку 
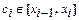и вычислим значение функции в этой точке, т. е. 
;
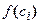3. Умножим найденное значение 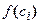на длину 
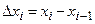соответствующего частичного отрезка: 
;
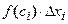4. Составим сумму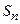 
всех таких произведений:
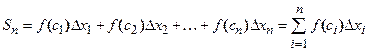, (1)
Сумма 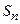называется интегральной суммой функции 
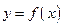на отрезке 
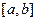. Обозначим через 
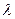длину наибольшего частичного отрезка: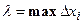 
.
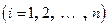5. Найдем предел интегральной суммы, когда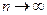 
, так что
.
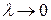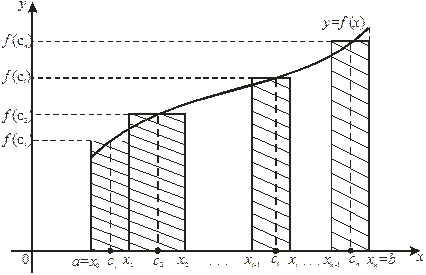
Рис. 1
Если при этом интегральная сумма 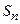имеет предел I, который не зависит от способа разбиения отрезка 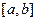на частичные отрезки, ни от выбора точек на них, то число I называется определенным интегралом от функции 
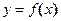на отрезке 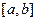и обозначается 
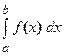. Таким образом,
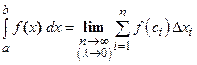. (2)
В этом случае функция 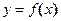называется интегрируемой на 
. Числа а и b называются соответственно нижним и верхним пределами интегрирования, 
– подынтегральной функцией,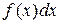 
– подынтегральным выражением, 
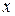– переменной интегрирования, отрезок называется областью (отрезком) интегрирования.
|
|
|
Теорема 1. Если функция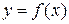 
непрерывна на отрезке , то она интегрируема на этом отрезке.
