Геометрический смысл определенного интеграла

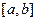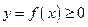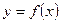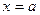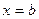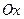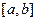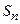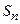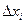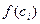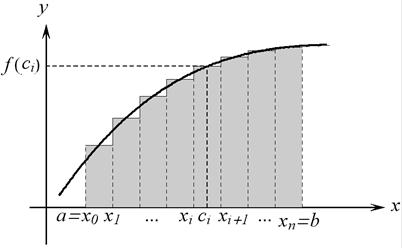
Пусть на отрезке задана непрерывная функция . Фигура, ограниченная сверху графиком функции , вертикальными прямыми и сбоку и осью снизу, называется криволинейной трапецией. Рассмотрим разбиение отрезка и соответствующую интегральную сумму (1). Слагаемые в (1) равны площадям прямоугольников с основаниями и высотами (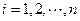), а вся сумма представляет площадь ступенчатой фигуры, образованной этими прямоугольниками (Рис. 2). Предел интегральных сумм (если он существует), то есть определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Рис. 2

Таким образом 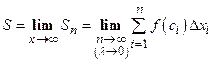, т. е. .

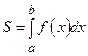Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.