1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: 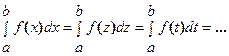 .
.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю 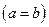 :
: 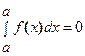 . Это свойство следует из определения интеграла.
. Это свойство следует из определения интеграла.
3. Если 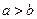 , то, при перестановке пределов интегрирования определенный интеграл меняет знак на противоположный
, то, при перестановке пределов интегрирования определенный интеграл меняет знак на противоположный 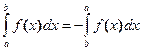 .
.
4. Постоянный множитель можно выносить за знак определенного интеграла:
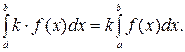
5. Определенный интеграл от алгебраической суммы двух (и более) функций равен алгебраической сумме определенных интегралов от этих функций:
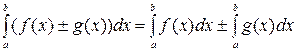 .
.
6. Если функция  интегрируема на
интегрируема на  и
и 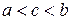 , то
, то 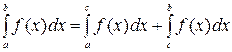 (аддитивность определенного интеграла).
(аддитивность определенного интеграла).
7. Если 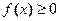
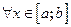 , то
, то 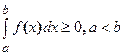 .
.
8. Если интегрируемые функции 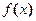 и
и 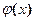 удовлетворяют неравенству
удовлетворяют неравенству 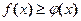
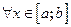 , то
, то 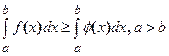 (определенность определенного интеграла).
(определенность определенного интеграла).
9. Если m и М – соответственно наименьшее и наибольшее значения функции 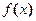 непрерывной на отрезке
непрерывной на отрезке 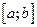 , то
, то 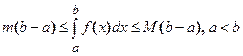 .
.
10. (Теорема о среднем). Если функция 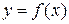 непрерывна на отрезке
непрерывна на отрезке  , то на этом отрезке существует точка
, то на этом отрезке существует точка 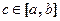 , такая, что
, такая, что 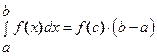 .
.
 2014-02-02
2014-02-02 1644
1644
