Формула Ньютона – Лейбница
Теорема 2. Если функция 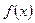 непрерывна на отрезке
непрерывна на отрезке 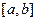 и
и 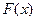 - какая-либо ее первообразная на этом отрезке, то имеет место формула:
- какая-либо ее первообразная на этом отрезке, то имеет место формула:
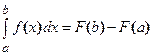 .
.
Равенство называется формулой Ньютона-Лейбница. Используя краткое обозначение 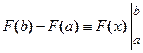 , эту формулу можно записать в виде
, эту формулу можно записать в виде
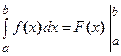 . (3)
. (3)
Таким образом, вычисление определенного интеграла от непрерывной функции сводится к отысканию ее первообразной, то есть, по существу, неопределенного интеграла.
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа:
1. На первом этапе находят некоторую первообразную 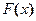 для подынтегральной функции
для подынтегральной функции 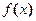 ;
;
2. На втором этапе находится разность 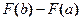 значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка 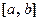 .
.
Пример 1. Вычислить интеграл 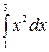 .
.
Решение: Для подынтегральной функции 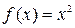 произвольная первообразная имеет вид
произвольная первообразная имеет вид  . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид:
. Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид: 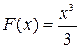 . Тогда
. Тогда 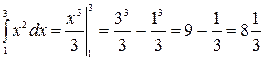 .
.
Пример 2. Вычислить интеграл 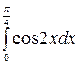 .
.
Решение: По формуле Ньютона-Лейбница имеем:
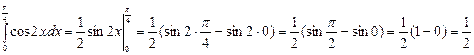 .
.
Пример 3. Найдем интеграл 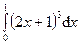 . Поскольку
. Поскольку 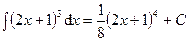 , то по формуле Ньютона-Лейбница получаем
, то по формуле Ньютона-Лейбница получаем 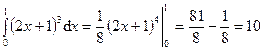 .
.
Пример 4. Площадь 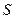 криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции 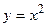 , осью
, осью 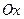 и прямыми
и прямыми 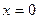 и
и 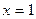 , равна
, равна 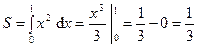 .
.
 2014-02-02
2014-02-02 1659
1659
