Общие сведения. Определение линейного векторного пространства

При рассмотрении многих вопросов ТЭС оказывается полезной геометрическая интерпретация постановки задачи, методов её решения и получения результатов. При этом описываемые громоздкими формулами соотношения между различными сигналами иллюстрируется ясными и наглядными геометрическими построениями. Аналогия между геометрическими векторами и сигналами не является случайной. Дело в том, что и геометрические векторы и сигналы можно рассматривать как элементы одной математической структуры – линейного векторного пространства. Поэтому, для изучения ТЭС необходимо иметь представления об основах теории линейных векторных пространств. В математике множество 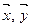называется линейным векторным пространством, удовлетворяющее следующим условиям:

1. для любых двух элементов 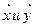однозначно определен третий элемент 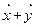, называемой их суммой и также входящий в данное множество, причем

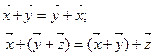
2. множество содержит нулевой элемент 0 такой, что .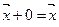

3. для каждого элемента 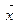линейного пространства существует противоположный ему элемент 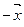такой, что .

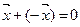4. любой элемент пространства 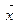можно умножить на число a из некоторого множества скаляров 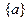, причем 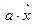также принадлежит данному пространству, и выполняются соответствия:

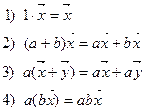
Записываемые формулы 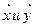- это элементы пространства, а a и b – скаляры. Множество скаляров образуют алгебраическую структуру, называемую полем. В качестве множества скаляров может выступать множество рациональных, комплексных и действительных чисел. При определении пространства обычно говорят так: линейное векторное пространство над полем (и указывается тип поля). Элемент любого векторного пространства называется вектором. Примеры линейных пространств:

1. множество геометрических векторов (пространство над полем действительных чисел), т.е. направленных отрезков с обычным определением векторного сложения и умножения и умножения вектора на число.

2. множество функций (пространство над полем комплексных чисел) с обычным определением и умножения на комплексное число.

3. множество упорядоченных последовательностей из n-чисел а₁, а₂, …, а_n.

4. пространство над конечным полем G F(n). В этом случае, элементы поля – векторы – представляют собой последовательности чисел а₁, а₂, …, а_n, выбираемое из поля G F(n). Такие пространства используются в теореме кодирования.

Подмножество элементов векторного пространства, обладаемое всеми свойствами векторного пространства, называется подпространством.