Функциональные пространства Евклида, Гильберта, Хемминга

Вещественным Евклидовым пространством R_n называется линейное n-мерное векторное пространство, любой вектор 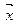которого определяется совокупностью конечного числа n его действительных координат 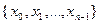как 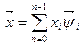(*1), где 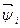- единичный базисный вектор. Пространство R_n можно определить как множество точек, представленных концами векторов, для которых 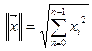, где 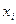– координаты вектора. При n = 2, n = 3 Евклидово пространство представляет собой обобщение соответственно двухмерного и трехмерного пространств геометрических векторов, в которых норма имеет смысл длины вектора. Расстояние между двумя векторам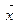и и 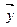определяется как норма разностей векторов:

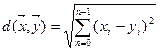
Скалярное произведение в этом пространстве определяется как:

,

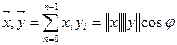где φ- угол между векторам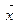и и .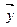

Зримо, этот угол может быть представлен в пространстве геометрических векторов при n = 2, n = 3. Для проекции вектор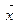а на 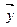и обратно имеем:

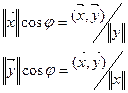
Координаты вектора x_i в (*1) представляет собой его проекции на направление координат осей, т.е на векторы базиса 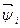. Из определения скалярного произведения вытекает неравенство Бунеаковского – Шварца:

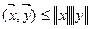
Знак равенства имеет место, когда 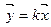, где k – скаляр, когда векторы 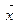и 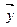коллениарны. Для соответствующих сигналы x(t) и y(t) это означает, что они совпадают по форме. При 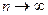R_n переходит в бесконечномерное пространство Гильберта L₂. Гильбертово пространство в частности пространство непрерывных комплексных функций действительного аргумента T, заданных на интервале (–T/2; T/2), в котором скалярное произведение определено соответствием:

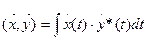
где 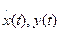– комплексная функция времени, а знак «*» – комплексное сопряжение.

Квадрат нормы в пространстве L₂:

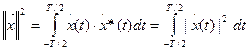
Эта величина имеет не только геометрический, но и физический смысл. Если действительный сигнал x (t) электрический ток в единичном сопротивлении 1 Ом, то 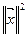определяет энергию сигнала E_x:

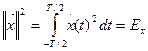
Элементы Гильбертова пространства L₂ характеризуются интегрируемым квадратом, т.е., если элементы этого пространства – действительные сигналы x (t), определенные на интервале (–T/2; T/2), то выполняется условие:

(*)

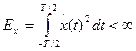Гильбертово пространство при этом обозначается как L₂ (T). При Т → ∞ получаем пространство L₂ (∞). Для некоторых сигналов векторов пространства L₂ (∞) условие (*) может не выполняться, но выполняется условие:

(**)

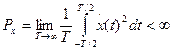В этом случае вводится скалярное произведение с размерностью мощности Р_х (для токов и напряжений с единичным сопротивлением):

(***)

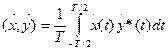При этом квадрат нормы:

(****)

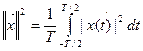При выполнении условия (***) в пространстве L₂ (∞) определены соотношения (***) и (****) при Т → ∞. Квадрат расстояния между двумя векторами в вещественном пространстве L₂ (T) определяется соотношениями:

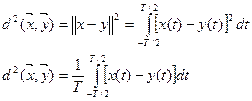
Пространство L₂ представляет собой естественное обобщение пространства R_n, получаемое путем перехода от дискретной функции непрерывного аргумента. В курсе ТЭС пространство L₂ имеет особое значение, т.к. оно позволяет применить общие геометрические представления к сообщениям, сигналам и помехам, определенным как функция непрерывного аргумента. Устремляя в (*1) n→ ∞, получаем представление x (t) в пространстве Гильберта:

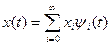
Важную роль в теории кодирования играет пространство Хемминга, элементами (векторами) которого являются двоичные n-разрядные кодовые комбинации .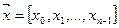

Пример: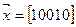

n=5

Сложение векторов в этом пространстве реализуется как поразрядное сложение элементов кодовой комбинации по модулю 2.

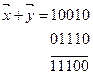
Пространство Хемминга определено над полем GF (2), т.е. множество скаляров, с которыми взаимодействует данное пространство, содержит 2 элемента – 1 или 0.

Скалярное произведение в этом пространстве задается как:

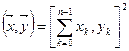
где сумма понимается в обычном смысле, а не по модулю 2. Отсюда норма двоичного вектора:

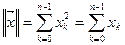
т.к. 1² =1 и 0² = 0.

Можно видеть, что норма двоичного вектора определяется количеством содержащихся в нем 1. Эту норму называют также весом вектора W. Расстояние в пространстве Хемминга:

,

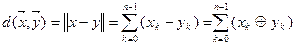где 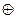– суммирование по модулю 2.

В поле GF (2) сложение по модулю 2 и вычитание по модулю 2 эквивалентно. Из этого определения следует, что в пространстве Хемминга расстояние между двоичными векторами определяется по числу позиций кодовой комбинации, в которых вектора имеют разные символы.