Ортогональность элементов в пространстве

Если скалярное произведение двух элементов 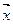и 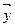равно 0, то элементы 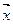и 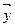называются ортогональными. В геометрическом пространстве векторов ортогональность означает, что проекция одного вектора на другой равна 0, т.е. вектора перпендикулярны. Подмножество элементов 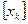называется ортогональной проекцией, если любые два его элемента 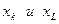попарно ортогональны, т.е.:

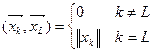
Элементы ортогональной системы линейно-независимы. Действительно, условием линейной независимости ненулевых элементов {x₁, x₂, …, x_n} является то, что 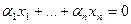выполняется только при нулевых значениях 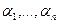. Предполагая, что {x₁, x₂, …, x_n} – ненулевые элементы ортогональной системы, умножим скалярно правую и левую часть последнего равенства на x₁. В результате, 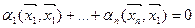. В силу условия ортогональности, все скалярные произведения, кроме первого, фигурирующие здесь, равны 0.

Поэтому .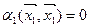

Поскольку 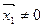, это значит, что 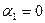. Т.к. тоже самое можно получить для всех 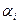, из этого следует линейная независимость элементов ортогональной системы. В любом n-мерном Евклидовом, Гильбертовом пространстве или пространстве Хемминга можно построить полный ортогональный базис, т.е. систему из n-ортогональных векторов.

Ортогональный базис, удовлетворяющий условию:

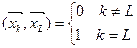
называется ортонормированным. Очевидно, что по любому ортогональному базису можно построить ортонормированный, заменив 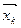на 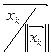. При этом векторы 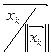называются ортами (единичный вектор вдоль оси).