2014-02-02
799
Пусть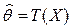 
- несмещённая оценка параметра 
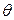, следовательно используя определение несмещённости можем записать: 
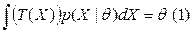. Положим: 
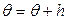и запишем равенство (2): 
.
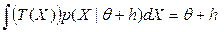Из условия нормировки плотностей можно записать: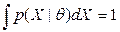 
и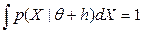 
. Оба условия нормировки умножим справа и слева на 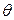и получим равенство:
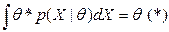и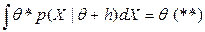 
.
Вычтем из (1) – (*):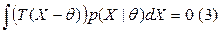
.
Вычтем из (2) – (**):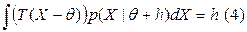
.
Из (4) вычтем (3):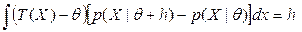 
. Левую часть последнего равенства домножим и разделим на одно и тоже выражение и разделим на одно и тоже выражение: 
.
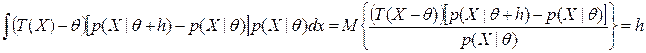Справедливо неравенство Шварца: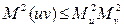 
. 
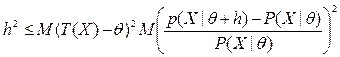, где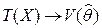 
. 
.
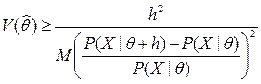Данная формула справедлива для любого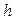 
.
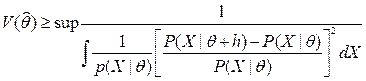
называется неравенство Чепмена - Роббина.
